一、拉普拉斯变换的定义
- 数学公式
$$ F(s) = \mathcal L\lbrace f(t) \rbrace = \int_0^{+\infin} f(t)e^{-st}dt $$
- $t$ 代表时域
- 由于$e$没有量纲,所以$s$代表频率
- 解释
- 将时域变为频域
二、阶跃函数与斜坡函数
2.1 单位阶跃函数图示
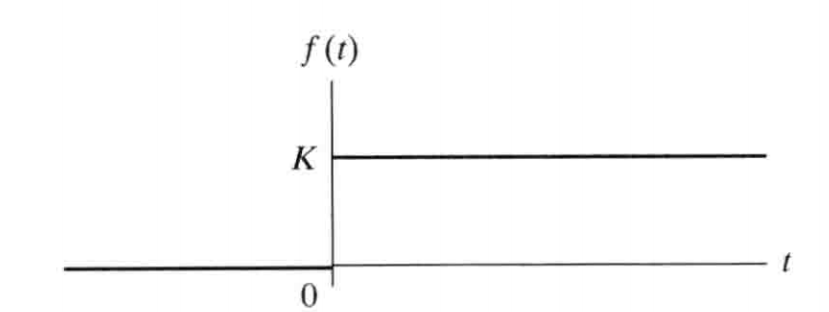
2.2 阶跃函数数学定义
$$ \begin{cases}Ku(t-a) =0 & t \lt a \\ Ku(t-a) = K & t \ge a \end{cases} $$
- 若需要定义从$a^-$到$a^+$的过渡是线性的(非突变),则可以假设
$$ Ku(0) = 0.5K \\\ \\ u(t) = \begin{cases} 0 & t \lt 0 \\ 1 & t \ge 0 \end{cases} \\\ \\ u(t) = \frac{dr(t)}{dt} $$
2.3 单位斜坡函数
- 定义
$$ r(t) = tu(t) = \int_{-\infin}^t u(\lambda)d\lambda $$
三、冲激函数
3.1 作用
定义间断点处的导数及其拉氏变换
3.2 举例
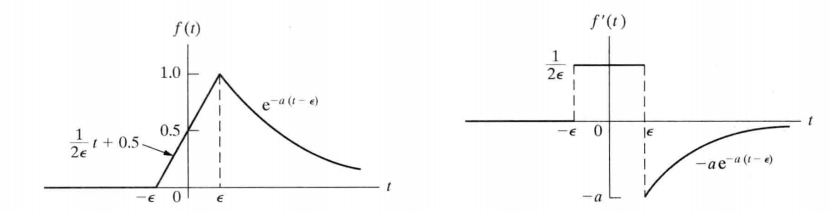
$$ f(0) \rightarrow \delta(t),\epsilon \rightarrow 0 \\\ \\ \delta(t)即为冲激函数 $$
3.3 条件
冲激函数是由可变参数函数的参数$\rightarrow 0$时形成的
-
幅值趋于$\infin$
-
函数持续时间趋于0
-
当参数变化时,函数下的面积为常数
- 在此例中,面积为1
$$ f(t) = \frac{K}{2\epsilon} e^{-|t|/\epsilon} $$
3.4 定义
$$ \int_{-\infin}^{+\infin} K \cdot \delta (t) dt = K \\\ \\ \delta(t) = 0, t \ne 0 \\\ \\ \delta(t) = \underset{\tau \rightarrow 0 }{lim} \frac{1}{\tau}rect\Big(\frac{t + \frac{\tau}{2}}{\tau}\Big) $$
3.5 特性
- 筛选特性
$$ \int_{-\infin}^{+\infin} f(t)\delta(t-a)dt = f(a) \\\ \\ I =\int_{-\infin}^{+\infin} f(t)\delta(t-a)dt = \int_{a-\epsilon}^{a+\epsilon}f(t)\delta(t-a) dt $$
- 冲激函数的拉氏变换
$$ \mathcal L \lbrace \delta(t) \rbrace = \int_0^{+\infin} \delta(t)e^{-st}dt = e^{-st}\Big|_{t=0} = 1 $$
- 冲激函数微分的拉氏变换

-
(a)图说明了冲激函数的生成过程
-
(b)图是冲激函数的微分
-
冲激函数微分的拉氏变换
$$ \mathcal L \lbrace \delta’(t) \rbrace = \underset{\epsilon \rightarrow 0}{lim}\int_{-\epsilon}^{0^-}\frac{1}{\epsilon^2}e^{-st}dt + \int_{0^+}^\epsilon \frac{1}{\epsilon^2}e^{-st}dt \\\ \\ = \underset{\epsilon \rightarrow 0}{lim} \frac{e^{-s\epsilon}+e^{-s\epsilon}-2}{s\epsilon^2} \\\ \\ = \underset{\epsilon \rightarrow 0}{lim} \frac{s^2(e^{-s\epsilon}+e^{-s\epsilon})}{2s} \ \ (洛必达法则) \\\ \\ = s \\\ \\ 同理可得:\mathcal L \lbrace \delta^{(n)}(t)\rbrace = s^n $$
- 冲激函数是阶跃函数的导数
$$ \delta(t) = \frac{du(t)}{dt} $$
四、函数变换
4.1 定义
- 说明
典型时域变换的拉普拉斯变换
- 因为要限制其为单边变换,所以设所有函数在$t\lt 0^-$时为0
4.2 常见函数的拉氏变换
- 单位阶跃函数的拉氏变换
$$ \mathcal L \lbrace f(t)\rbrace = \int_{0^-}^{+\infin} f(t)e^{-st} dt = \int_{0^+}^\infin 1e^{-st} dt = \frac{1}{s} \\\ \\ $$
- 衰减指数函数的拉氏变换
$$ \mathcal L \lbrace e^{-at} \rbrace = \int_{0^+}^{+\infin} e^{-at}e^{-st}dt = \frac{1}{s+a} $$
- 正弦函数的拉氏变换
$$ \begin{align} \mathcal L \lbrace sin\omega t\rbrace & = \int_{0^-}^{\infin} sin(\omega t)e^{-st}dt \\\ & = \int_{0^-}^{+\infin} \frac{e^{j\omega t}-e^{-j\omega t}}{2j}e^{-st}dt \\\ & = \frac{\omega}{\omega^2 + s^2} \end{align} $$
4.3 拉氏变换对简表
| 类型 | $f(t),t\gt 0^-$ | $F(s)$ |
|---|---|---|
| 冲激函数 | $\delta(t)$ | 1 |
| 阶跃函数 | $u(t)$ | $1/s$ |
| 斜坡函数 | $t$ | $1/s^2$ |
| 指数函数 | $e^{-at}$ | $1/(s+a)$ |
| 正弦函数 | $sin(\omega t)$ | $\frac{\omega}{\omega^2 + s^2}$ |
| 余弦函数 | $cos(\omega t)$ | $\frac{s}{s^2+\omega^2}$ |
| 衰减斜坡函数 | $te^{-at}$ | $\frac{1}{s^2+a^2}$ |
| 衰减正弦函数 | $e^{-at}sin(\omega t)$ | $\frac{\omega}{(s+a)^2+ \omega^2}$ |
| 衰减余弦函数 | $e^{-at}cos(\omega t)$ | $\frac{s+a}{(s+a)^2 + \omega^2}$ |
五、算子变换
5.1 常数与加减运算
$$ \mathcal L \lbrace Kf(t)\rbrace = KF(s) \\\ \\ \begin{align} \mathcal L \lbrace f_1(t) + f_2(t) - f_e(t) \rbrace = F_1(s) + F_2(s) - F_3(s) \end{align} $$
5.2 微分与积分
$$ \begin{align} \mathcal L \Big\lbrace \frac{df(t)}{dt} \Big\rbrace & = sF(s) - f(0^-) \\\ \mathcal L \Big\lbrace \int_{0^-}^t f(x)dx \Big\rbrace & = \int_{0^-}^{+\infin} \Big[\int_{0^-}^t f(x)dx\Big]e^{-st}dt \end{align} $$
5.3 时域平移
六、脉冲函数
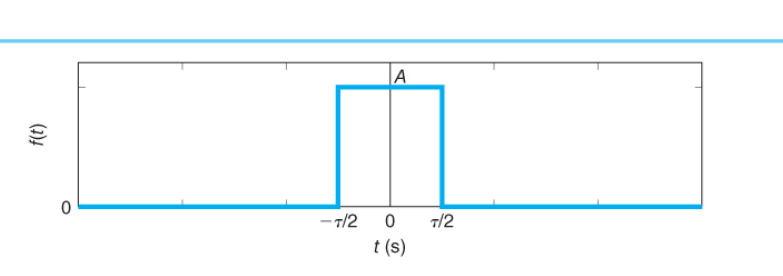
6.1 方形脉冲
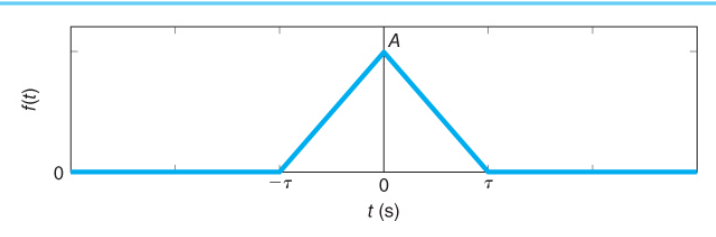
$$ f(t) = A \ rect(\frac{t}{\tau}) $$
- $A$表示脉冲,$\tau$表示宽度,零值点表示中点
6.2 三角脉冲
$$ f(t) = A \ tri \Big(\frac{t}{\tau}\Big) $$
- $A$表示脉冲,$2\tau$表示宽度,零值点表示中点