正弦信号源 正弦响应
表达
$$ v =V_mcos(\omega t+\phi) \ [1] \\\ \\ f =\frac{1}{T} \\\ \\ \omega=2\pi f =\frac{2\pi}{T} \\\ \\ 均方根V_{rms} = \sqrt{\frac{1}{T} \int_{t_0}^{t_0+T}V_m^2cos^2(\omega t +\phi)dt} \\\ \\ 对于[1],均方根为\frac{V_m}{\sqrt{2}} $$
正弦响应
正弦电源激励下的RL电路
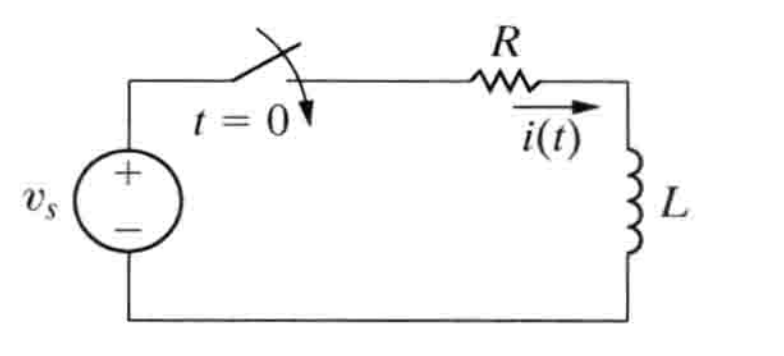
电流与时间
$$ L\frac{di}{dt} + Ri = V_mcos(\omega t + \phi) \Rightarrow \\\ \\ i = \frac{-V_m}{\sqrt{R^2+\omega^2L^2}}cos(\phi -\theta)e^{-(R/L)t}+\frac{V_m}{\sqrt{R^2+\omega^2L^2}}cos(\omega t + \phi - \theta) $$
稳态响应的性质
-
稳态响应为一正弦函数
-
响应频率与信号源频率相同
-
稳态响应的最大值$\neq$ 信号源的幅值
-
稳态响应的相位角与信号源的不同
相量 频域
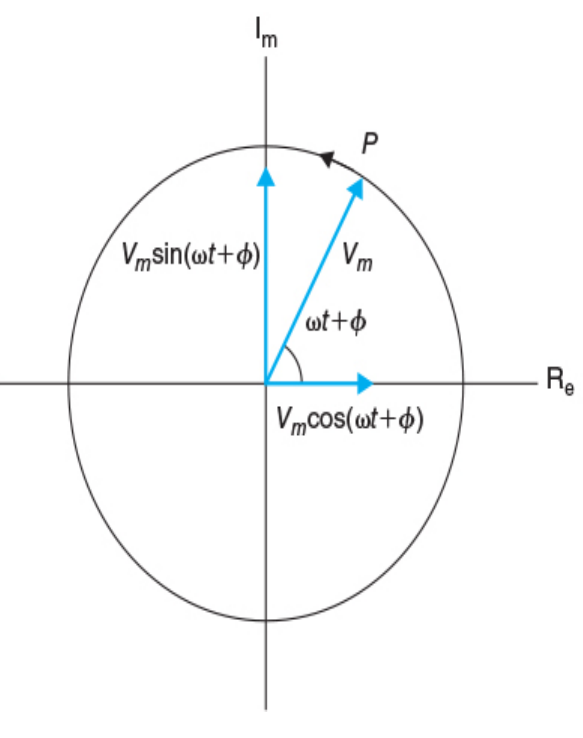
正弦信号源的相量
$$ 欧拉定律: e^{\pm j \theta} = cos\theta \pm j\cdot sin\theta \\\ \\ \therefore v = V_mcos(\omega t +\phi) = V_m \Re\lbrace e^{j(\omega t +\phi)} \rbrace = \Re\lbrace{V_me^{j\omega t}\cdot e^{j\phi}}\rbrace \\\ \\ 相量\pmb V = V_me^{j\phi} =P\lbrace{V_mcos(\omega t + \phi)}\rbrace \\\ \\ \pmb V = V_mcos\theta + jV_msin\theta \\\ \\ 注意, 1e^{j\phi} = 1 \angle{\phi}^{\circ} $$
相量算术
$$ 加减法 \\\ \\ 将向量转换为复数形式加减 \\\ \\ \pmb{乘除法} \\\ \\ \pmb{V_a\angle{\phi}^{\circ} \pm V_b\angle{\theta}^{\circ} = V_aV_b\angle({\phi \pm \theta})^{\circ}} $$
反相量变换
- 定义
$$ P^{-1}\lbrace V_me^{j\phi}\rbrace = \Re \lbrace V_m e^{j\omega t} e^{j\phi}\rbrace $$
- 相量法的特点
$$ 如果V = \sum_{i=1}^n V_i\Rightarrow \pmb{V = \sum_{i=1}^n V_i} $$
频域下的无源电路元件
伏安特性
$$ i =I_mcos(\omega t + \phi) \\\ \\ 对于电阻\\\ \\ \pmb V=R\pmb I \\\ \\ 对于电感 \\\ \\ v = L\frac{di}{dt} = -\omega LI_msin(\omega t + \phi) = -\omega L I_m cos(\omega t +\phi -\frac{\pi}{2}) \\\ \\ \pmb V = -\omega L I_m e^{j(\phi - \frac{\pi}{2})} = -\omega L I_m e^{j\phi}e^{j(-\pi/2)} = j\omega I_m L e^{j\phi} = j\omega L \pmb I \\\ \\ 对于电容 \\\ \\ \pmb V =\frac{1}{j\omega C} \pmb I = -\frac{j}{\omega C} \pmb I $$
阻抗和电抗
- 定义
阻抗是一种电气参数,表示一个电路中电流和电压之间的相对关系,它是一个复数量,由实部和虚部组成。
电抗是一种电气参数,表示一个电路中电流和电压之间的相对关系,但它只是一个实数量,只由实部组成。
- 阻抗与导纳
$$ \pmb V = Z\pmb I \\\ \\ Z = R + jX \\\ \\ Z: Impedence \ R: resistance \ X: reactance \\\ \\ Y = G +jB \\\ \\ Y: Admittance \ G: Conductance \ B: susceptance $$
- 阻抗和电抗
| 电路元件 | 阻抗 | 电抗 |
|---|---|---|
| 电阻 | $R$ | - |
| 电感 | $j\omega L$ | $\omega L$ |
| 电容 | $\frac{1}{j\omega C}$ | $-1/\omega C$ |
串并联 三角形-星形变换
并联阻抗与串联阻抗的合并
串联阻抗
$$ Z_{ab}=\sum_{i=1}^n Z_i $$
并联阻抗与串联阻抗的合并
- 公式
$$ 导纳 Y= \frac{1}{Z_{ab}}=\sum_{i=1}^n\frac{1}{Z_i} \\\ \\ Y = \frac{1}{Z} = G +jB(S) $$
- 导纳和电纳
| 电路参数 | 导纳 | 电纳 |
|---|---|---|
| 电阻 | G | - |
| 电感 | $j(-1/\omega L)$ | $-1/\omega L$ |
| 电容 | $j\omega C$ | $\omega C$ |
三角形-星形变换
- 图示
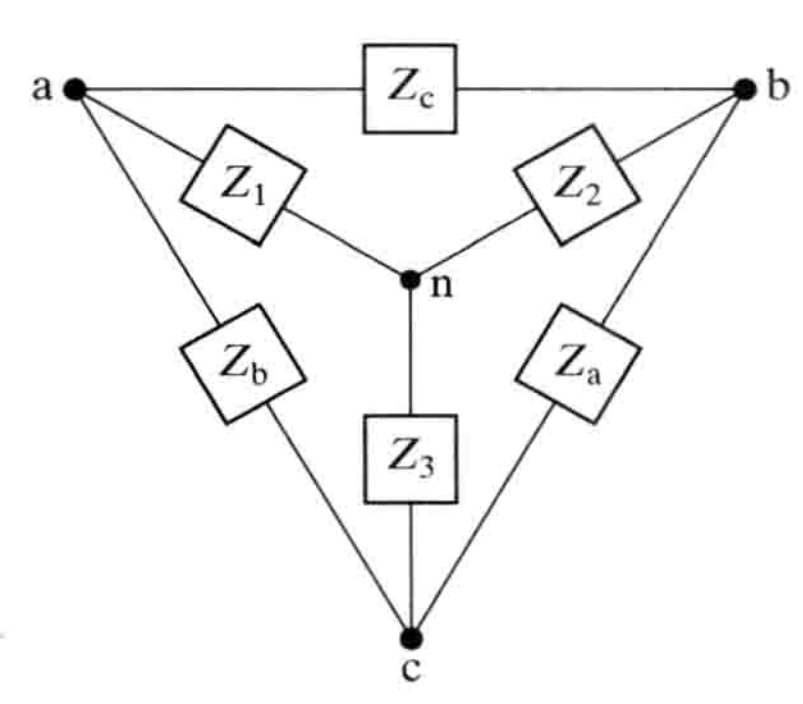
- 关系
- 与时域下的关系一样一样
电源变换 戴维南-诺顿等效电路
- 具体情况与时域下的相同
变压器
线性变压器电路
- 电路图
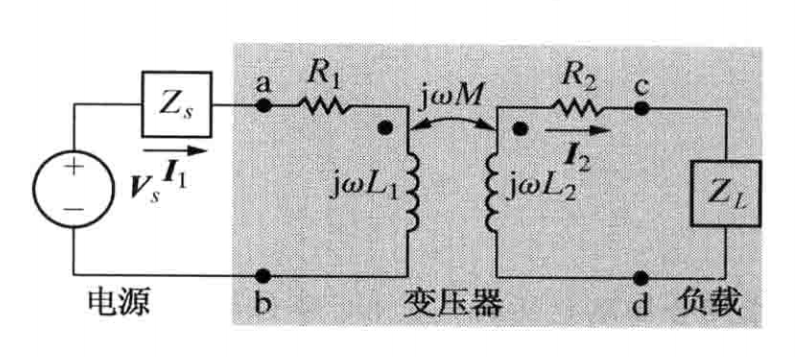
- 推导
$$ 左边电路KVL方程: \pmb {V_s} = \pmb I_1(Z_s + R_1 + j\omega L_1 ) - j\omega M\pmb I_2 \\\ \\ 右边KVL方程 :\pmb{I_2}(R_2+Z_L+j\omega L_2) - j\omega M \pmb{I_1} = 0 \\\ \\ 令 Z_{11} = Z_s+R_1+j\omega L_1, Z_2 = Z_L+R_2 + j\omega L_2 \\\ \\ 我们可以得到 $$
- 结论
$$ \pmb I_1 =\frac{Z_{22}}{Z_{11}Z_{22}+\omega^2M^2} \pmb V_s \\\ \\ \pmb I_2 = \frac{j\omega M}{Z_{11}Z_{22}+\omega^2M^2}\pmb V_s = \frac{j\omega M}{Z_{22}}\pmb I_1 \\\ \\ 对于电源内部, Z_{int} = \frac{V_s}{I} = Z_{11}+ \frac{\omega^2M^2}{Z_{22}}\\\ \\ Z_{ab} = Z_{11} + \frac{\omega^2 M^2}{Z_{22}}-Z_s = R_1+j\omega L_1 + \frac{\omega^2 M^2}{(R_2+j\omega L_2+Z_L)} [1] $$
- 反射阻抗
$$ [1]式中的Z_r =\frac{\omega^2 M^2}{(R_2+j\omega L_2+Z_L)}被称为\pmb{反射阻抗} \\\ \\ 将Z_L=R_L+jX_L \\\ \\ 得到Z_r = \frac{\omega^2 M^2}{|Z_{22}|^2}[(R_2+R_L)-j(\omega L_2 + X_L)] $$
理想变压器
- 前提
-
耦合系数为1($k=1$)
-
$L_1 = L_2 \rightarrow +\infin$
-
寄生电阻造成的线圈损失忽略不计
- 继续推导
$$ 当耦合为紧耦合时,两磁通相同 \\\ \\ \frac{L_1}{L_2} = (\frac{N_1}{N_2})^2 \\\ \\ \because L_1 = L_2 \rightarrow +\infin \\\ \\ \therefore X_{ab} = (\frac{N_1}{N_2})^2 X_L \\\ \\ Z_{ab} = R_1 + (\frac{N_1}{N_2})^2 R_2 + (\frac{N_1}{N_2})^2 (R_L + jX_L) \\\ \\ $$
- 电流比与电压比
$$ \frac{V_1}{N_1} = \frac{V_2}{N_2} \\\ \\ I_1N_1 = I_2N_2 $$
- 理想电压器的阻抗匹配
-
图示
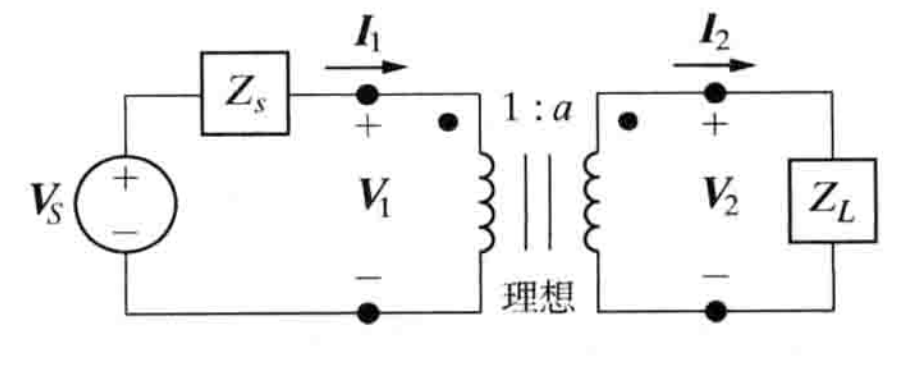
-
关系
$$ 令 a = \frac{N_1}{N_2} \\\ \\ 易知\frac{V_1}{I_1} = a^2 \frac{V_2}{I_2} = a^2 Z_L\\\ \\ Z_{IN} = \frac{V_1}{V_2}= a^2Z_L \\\ \\ 即:理想变压器的次级线圈的负载阻抗以水平因子a^2反映到了初级线圈上 $$