Signal Power & Energy
- 注: 此处的能量与功率是一个相对值,单位不定
信号分类
| Continuous Signal | Discrete Signal |
|---|---|
| $x(t)$ | $x(n)$ |
信号能量与功率
基于信号/功率大小的分类
| Finite Power System | 能量不是无穷 |
|---|---|
| Finite Energy System | $P \rightarrow 0$ |
| Infinite Power System | $P \rightarrow \infin, E \rightarrow \infin$ |
关系
- Continuous Signal
$$ \begin{aligned} E_{\infin} & \equiv \underset{t \rightarrow \infin}{lim}\int_{-t}^{t}|x(t)|^2dt \\ P_{\infin} & \equiv \underset{t \rightarrow \infin}{lim}\frac{1}{2t} \int_{-t}^{t}|x(t)|^2dt \\ \end{aligned} $$
- Discrete Signal
$$ \begin{aligned} E_{\infin} & \equiv \underset{n \rightarrow \infin}{lim} \sum_{-n}^n|x[n]|^2dn \\ P_{\infin} & \equiv \underset{n \rightarrow \infin}{lim}\frac{1}{2n + 1} \sum_{-n}^n |x[n]|^2dn \\ \end{aligned} $$
独立变量的初级转换
转换类型
$$ \begin{aligned} x(t) \longrightarrow x(\alpha t + \beta) \end{aligned} $$
| time shift | 在$\beta \neq 0$时平移 |
|---|---|
| time reversal | 在$\alpha <0$时翻转 |
| time scaling | 在$|\alpha| < 1$时stretch, 在$|\alpha| > 1$时compress |
周期信号 奇偶信号
| periodic Signals(重要的周期信号求解方法) | $x(t) = x(t+T)$ |
|---|---|
| Odd & Evene Signals | Even: $x(t) = x(-t)$, Odd: $-x(t) = x(-t)$ |
- 任何信号函数可以拆分成$O(t) + E(t)$
$$ \begin{aligned} E(x) &= \frac{1}{2}(x(t) + x(-t)) \\ O(x) &= \frac{1}{2}(x(t) - x(-t)) \\ x(t) &= E(x) + O(x) \end{aligned} $$
指数信号
连续指数信号
| 指数 | $x(t) = Ce^{at}, C, a \in \mathbb C$ |
|---|---|
| 正弦 | $x(t) = Acos(\omega t + \phi)$ |
指数信号的虚数部分必然是周期信号
$$ \begin{aligned} x(t) &= e^{j\omega t} \\ if \ t &= 0: \\ x(t) &= 1 \\ T = 0 \\\ \\ elif \ t &\neq 0: \\ x(t) &= e^{j\omega t} \\ &= cos(\omega t) + jsin(\omega t) \\ T &= \frac{2\pi}{\omega} \end{aligned} $$
指数信号虚数部分的E/P
$$ \begin{aligned} E & = \int_{-t}^{t}|e^{j\omega t}|^2dt \\ &= 2t \\ P &= \frac{E}{2T} \\ &= 1 \end{aligned} $$
正弦信号的分解
$$ \begin{aligned} Acos(\omega t + \phi) &= \frac{A}{2}[e^{j\omega t}\cdot e^{j\phi} + e^{-j\omega t}\cdot e^{-j\phi}] \\ &= \mathbb R\lbrace e^{j(\omega t +\phi)}\rbrace \\ Asin(\omega t + \phi) &= \frac{A}{2}[e^{j\omega t}\cdot e^{j\phi} - e^{-j\omega t}\cdot e^{-j\phi}] \\ &= \mathbb I\lbrace e^{j(\omega t +\phi)}\rbrace \\ \end{aligned} $$
harmonically related complex exponentials
- 这些信号周期$T_i$的最大公约数为$T_0$
$$ \begin{aligned} T_i &= \frac{2\pi}{\omega_i} \\ T_0 &= \frac{2\pi}{\omega_0} \\ T_0 &= k T_i \\ x(t)_i &= e^{jk\omega t} \end{aligned} $$
考虑虚实结合的指数信号
$$ \begin{aligned} x(t) &= Ce^{at} \\ C&= |C| e^{j \theta} \\ a &= r + j \omega \\ x(t) &= |C|e^{j \theta} e^{(r + j\omega) t} \\ &= |C|e^{rt} e^{j(\omega t + \theta)} \end{aligned} $$
-
当$r = 0$,都是正弦信号
-
当$r \gt 0, r \lt 0$时
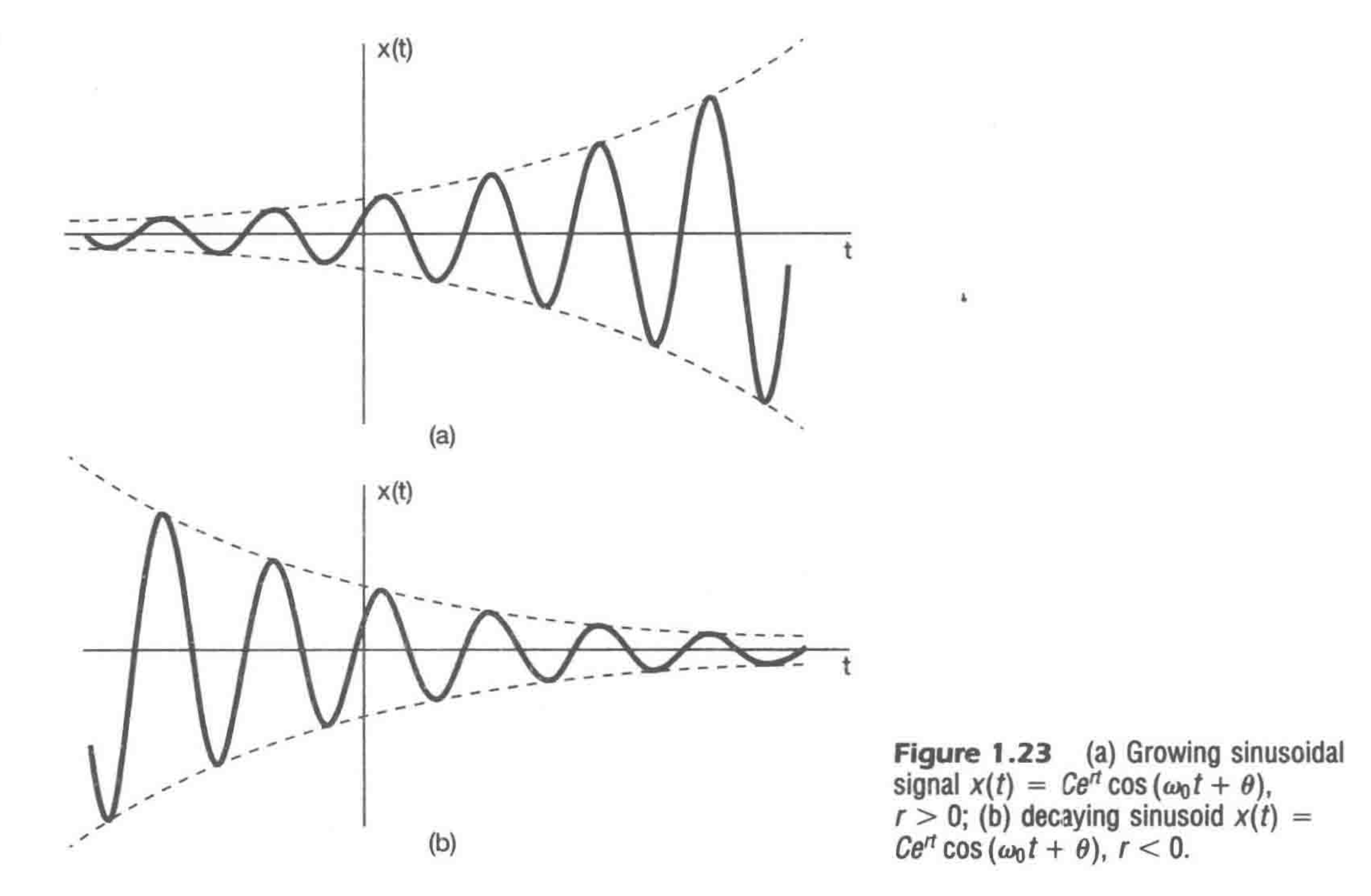
离散指数信号
$$ \begin{aligned} x[n] &= C\alpha^n \\ C &= |C| e^{j\theta} \\ \alpha &= |\alpha| e^{j\omega} \\ \therefore x[n] &= |C||\alpha|^n [cos(\omega n + \theta) + jsin(\omega n + \theta)] \end{aligned} $$
-
当$\alpha = 1$,都是正弦信号
-
当$\alpha \gt 1$, Decay
-
当$\alpha \gt 1$, Grow
Unit Impluse & Unit Step Functions
discrete unit impluse & unit step functions
方程
$$ \begin{aligned} \delta[n] &= \begin{cases} 0 & n \ne 0 \\ 1 & n = 0 \end{cases} \\ u[n] &= \begin{cases} 0 & n \lt 0 \\ 1 & n \ge 0 \end{cases} \end{aligned} $$
两者关系
$$ \begin{equation} \delta [n] = u[n] - u[n-1] \end{equation} $$
$$ \begin{equation} u[n] = \sum_{ k = 0}^{ n} \delta [n - k] \end{equation} $$
脉冲函数的其他属性
$$ \begin{equation} x[n]\delta[n] = x[0]\delta[n] \end{equation} $$
$$ \begin{equation} x[n] \delta [n- n_0] = x[n_0] \delta [n - n_0] \end{equation} $$
$$ \begin{equation} \delta ( \alpha t) = \frac{ 1 }{ | \alpha| } \delta (t) \end{equation} $$
$$ \begin{equation} x[n] * \delta [n] = x[n] \end{equation} $$
Continuous unit impluse & unit step functions
二者关系
- 基本关系
$$ \begin{equation} \delta (t) = \frac{ du(t) }{ dt } \end{equation} $$
$$ \begin{equation} u(t) = \int_{ - \infin }^{ t } \delta (\tau) d\tau \end{equation} $$
- 令$\sigma = t - \tau$
$$ \begin{equation} \begin{aligned} u(t) &= \int_{\infin}^0\delta(t-\sigma)(-d\sigma) \\ &= \int_0^\infin \delta(t-\sigma)d\sigma \end{aligned} \end{equation} $$

- 重要属性
- 缩放
$$ \begin{equation} ku(t) = \int_{-\infin}^tk\delta(\tau)d\tau \end{equation} $$
Basic System Properties
注意: 对于一个系统,输入和输出的时间分别指的是$y(t)$和$x(t)$当中的$t$
Memory
输出只和当前输入有关,叫做memoryless, 否则就是system with memory
Invertibility and Inverse System
- 定义
$x$和$y$一一对应
- 图示

Causality
输出仅取决于当前和过去的输入
- 若未来的输入可以影响输出,就不是Causality
Stability
Bounded Input $\rightarrow$ Bounded Output, $t \in \mathbb R$
- 特别注意,$\delta (t)$ Not Bounded(无界)
Time Invirance
时间平移不变性 $x(t) \longrightarrow y(t), x(t-t_0) \longrightarrow y(t-t_0)$
- LCCDE (Linear Constant Coefficient Equation)
Linearity
满足以下条件的系统是线性的
$$ \begin{aligned} x_k &\longrightarrow y_k \Longrightarrow\sum_k a_k x_k &\longrightarrow \sum_k b_k y_k \end{aligned} $$
Appendix
Trigonometric Formula
- 合并
$$ \begin{gather} \begin{aligned} asinx + bcosx &= \sqrt{a^2 + b^2}sin(x + \phi) \\ tan \phi &= \dfrac{sinx}{cosx} \end{aligned} \end{gather} $$
- 三角函数的复指数表达
$$ \begin{gather} \begin{aligned} cos(x) &= \frac{ e^{jx} + e^{-jx}}{ 2 } \\ sin(x) &= \frac{ e^{jx} - e^{-jx}}{ 2j } \end{aligned} \end{gather} $$
Plural Formula
$$ \begin{gather} \begin{aligned} 1 &= e^{j 2 \pi n} \\ (-1)^n &= e^{j \pi n} \\ j^n &= e^{j \dfrac{ \pi }{ 2 } n} \end{aligned} \end{gather} $$