Low Frequency Response of the Common-Source Amplifiers

CS Amplifier

电路

1. 原电路

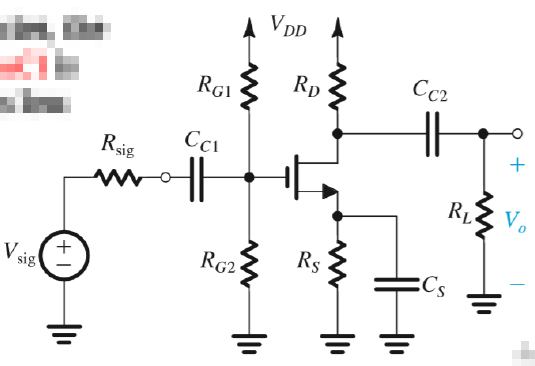
2. 变换电路

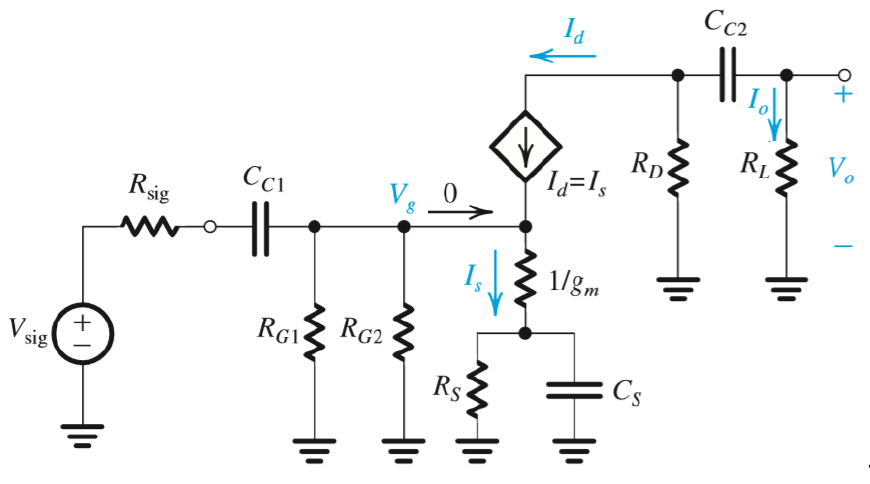
分析

$$ \begin{aligned} A_v &= \frac{V_o}{V_{i}} \\ &= \frac{V_o}{V_{sig}} \\ &= \frac{V_g}{V_{sig}} \frac{I_d}{V_g} \frac{V_o}{I_d} \\\ \\ V_g &= \frac{R_G}{R_G + \frac{1}{j\omega C} + R_{sig}}\\ &= V_{sig} \frac{R_G}{R_G + R_{sig}}\frac{j\omega}{j\omega + \frac{1}{C_{C1}(R_G + R_{sig})}} \\ \omega_{P1}&=\omega_0 \\

&= \frac{1}{C_{C1}(R_G + R_{sig})} \\\ \\ I_d &= I_S \\ &= \frac{V_g}{1/g_m + Z_S} \\ &= V_gg_m \frac{\frac{1}{C_SR_S} + j\omega}{\frac{g_mR_S + 1}{C_SR_S} + j\omega} \\ \omega_{P2} &= \omega_0 \\ &= \frac{g_m + 1/R_S}{C_S}\\\ \\ V_o &= I_oR_L \\ &= -I_d \frac{R_DR_L}{R_D + R_L + \frac{1}{j\omega C_{C2}}} \\ &= -I_d \frac{R_DR_L}{R_D + R_L}\frac{j\omega}{j\omega + \frac{1}{C_{C2}(R_D+R_L)}} \\ \omega_{P3} &= \omega_0 \\ &= \frac{1}{C_{C2}(R_D + R_L)} \\\ \\ A_v & = \frac{V_o}{V_{sig}} \\ &= -\frac{R_G}{R_G + R_{sig}} g_m R_L’ \Big( \frac{j\omega}{j\omega + \omega_{P1}} \Big) \Big( \frac{\omega_z + j\omega}{j\omega + \omega_{P2}} \Big) \Big( \frac{j\omega}{j\omega + \omega_{P3}} \Big) \\ &= A_M \Big( \frac{j\omega}{j\omega + \omega_{P1}} \Big) \Big( \frac{\omega_z + j\omega}{j\omega + \omega_{P2}} \Big) \Big( \frac{j\omega}{j\omega + \omega_{P3}} \Big) \\ 其中, A_M &= -\frac{R_G}{R_G + R_{sig}} g_m R_L’ \\ R_L’ &= R_L || R_D \end{aligned} $$

Frequency Response

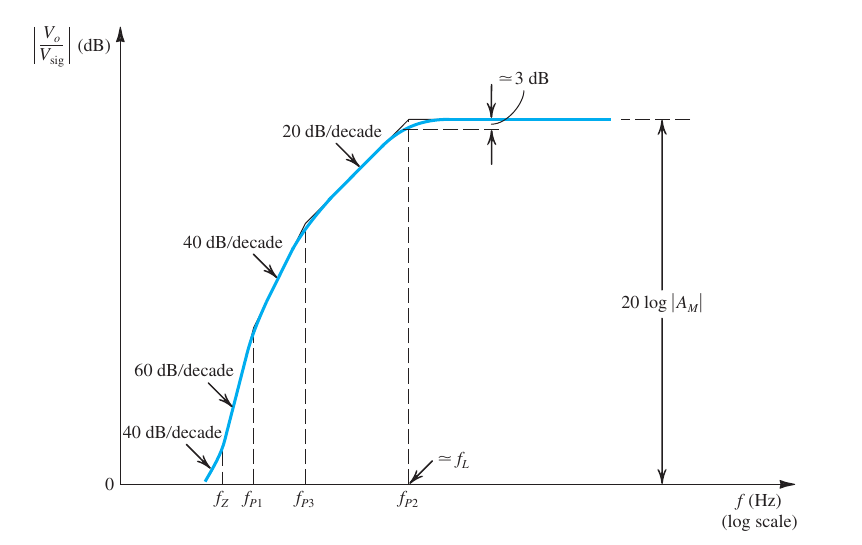
$$ \begin{aligned} 有&Dominant \ Pole \\ f_L &\approx f_{P2} \\ 无 &Dominant \ Pole \\ f_L &\approx \sqrt{f_{P1}^2 + f_{P2}^2 + f_{P3}^2 - 2f_Z^2} \\\ \\ 注意,\omega&=2\pi f \end{aligned} $$

The Method of Short-Circuit Time Constants

1. Let $V_{sig}= 0$

2. Consider the capacitors one at a time. That is,while considering capacitor $C_i$ , replace all the other capacitors with short circuits.

3. For each capacitor $C_i$, find the total resistance $R_i$ seen by $C_i$

4. Calculate the 3-dB frequency $f_L$

$$ f_L = \sum_{i=1}^n\frac{1}{R_i C_i} $$

Internal Capacitive Effects and the High-Frequency Model of the MOSFET

图示

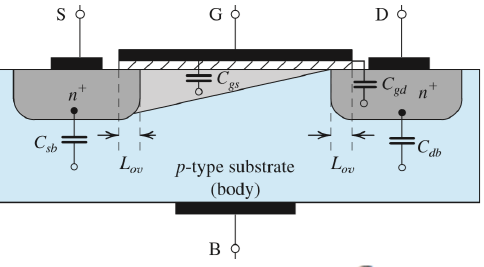
分析

$$ \begin{aligned} C_{ov} &= WL_{ov}C_{ox} \\ C_{gd} &= C_{ov} \\ C_{gs} &= \frac{2}{3} WLC_{ox} + C_{ov} \\ C_{sb} &= \frac{C_{sb0}}{\sqrt{1 + \frac{V_{SB}}{V_o}}} \\ C_{db} &= \frac{C_{db0}}{\sqrt{1 + \frac{V_{DB}}{V_o}}} \end{aligned} $$

• $_{ov}$意为overlap

• When the source is connected to the body, $C_{sb}=0$.

• $C_{db}$ can be neglected.

Other Models

hybrid-$\pi$ model

1. 电路

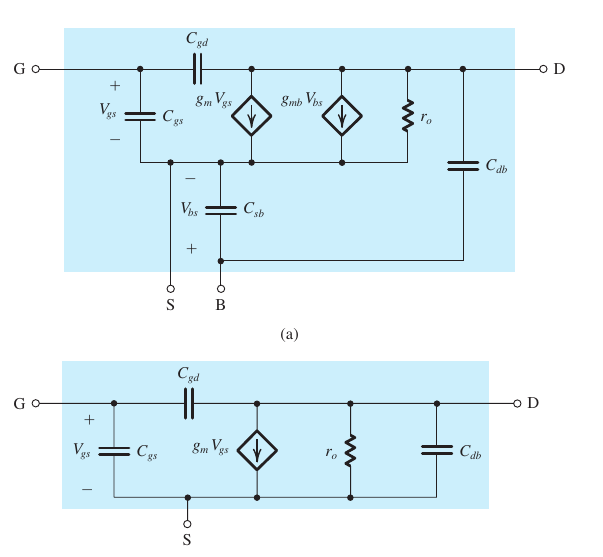
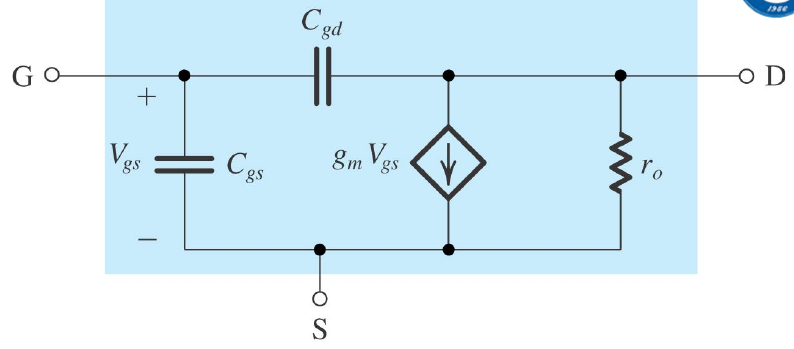
2. 分析

• (a)中S和B想连后得到(b)

• 为了简化分析，去掉$C_{db}$, 得到(c)

3. Hybrid-$\pi$ Model 又称 High-Frequency $\pi$ Model

simplified high-frequency T model

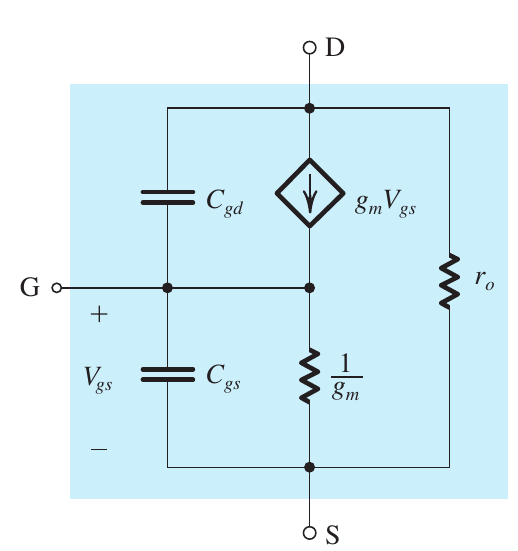
The MOSFET Unity-Gain Frequency ($f_T$)

电路

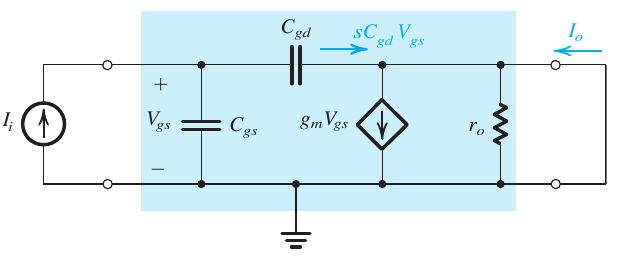
分析

$$ \begin{aligned} I_o &= g_mV_{gs} - sC_{gd}V_{gs} \\ &\approx g_m V_{gs} \\ V_{gs} &= \frac{I_i}{s(C_{gs} + C_{gd})} \\ \frac{I_o}{I_i} &= \frac{g_m}{s(C_{gs} + C_{gd})} \\ \Big|\frac{I_o}{I_i} \Big| &= \frac{g_m}{\omega(C_{gs} + C_{gd})} \\ \therefore \omega_T &= \frac{g_m}{C_{gs} + C_{gd}} \\ f_T &= \frac{\omega_T}{2\pi}\\ &= \frac{g_m}{2\pi (C_{gs} + C_{gd})} \end{aligned} $$

High-Frequency Response

CS Amplifier

电路 & 电路简化

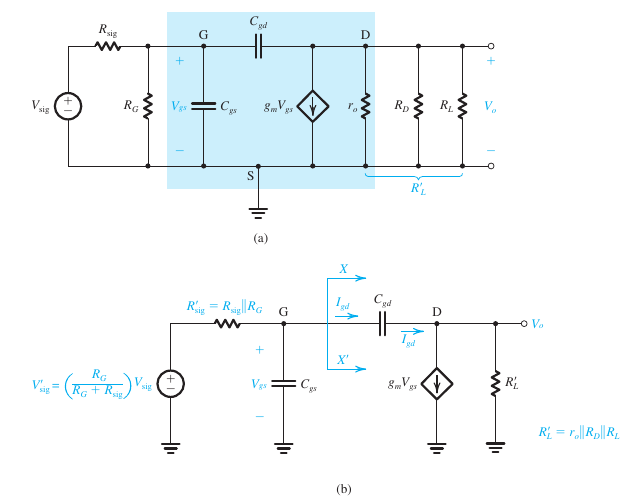
分析

$$ \begin{aligned} I_o &= g_mV_{gs} - I_{gd} \\ &\approx g_mV_{gs} \\ \therefore V_o &\approx -(g_mV_{gs})R_L’ \\\ \\ I_{gd} &= (V_{gs}-V_{sd})sC_{gd} \\ &= (V_{gs} - V_o)sC_{gd} \\ &= sC_{gd}(1 + g_m R_L’)V_{gs} \\\ \\ 为了让&I_{gd}看起来更简洁，我们把C_{gd}替换一下 \\ sC_{eq}V_{gs} &= sC_{gd}(1 + g_m R_L’)V_{gs} \\ \therefore C_{eq} &= (1 + g_mR_L’)C_{gd} \\ 于是，& C_{gd}被放大了很多倍 \end{aligned} $$

• 这种放大倍数被称为Miller Effect, $(1 + g_mR_L’)$被称作Miller Multiplier

$$ \begin{aligned} A_M &= - \frac{R_G}{R_G + R_{sig}} (g_m R_L’) \\ 结合CAD&的知识 \\ V_{gs} &=\frac{R_G}{R_G + R_{sig}} V_{sig} \frac{1}{1 + \frac{s}{\omega_0}} \\ \therefore \frac{V_o}{V_{sig}} &= \frac{R_G}{R_G + R_{sig}} \frac{1}{1 + \frac{s}{\omega_0}}(g_mR_L’) \\ &= A_M \frac{1}{1 + \frac{s}{\omega_0}} \\\ \\ 其中,\omega_H &= \omega_0 \\ &= \frac{1}{R_{sig}‘C_{in}} \\ f_H &= \omega_0/2\pi \\ &= \frac{1}{2\pi R_{sig}‘C_{in}} \end{aligned} $$

进一步等效

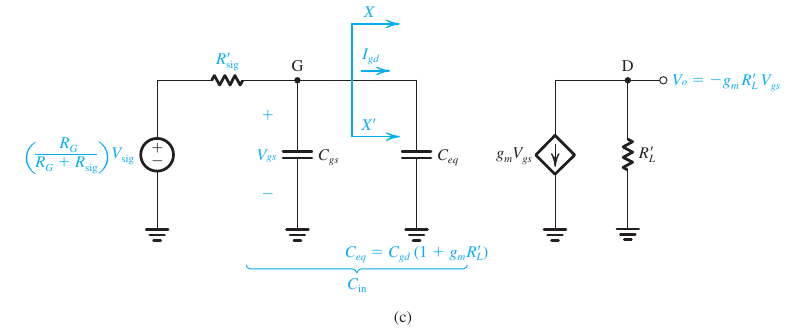
Frequency Response

$R_{sig}$ Is Low

1. 电路

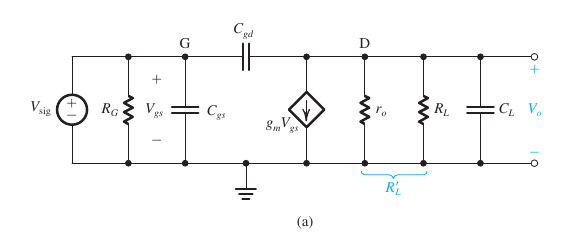
2. 分析

$$ \begin{aligned} V_{gs} &\approx V_{sig} \\ I_{gd} &= sC_{gd}(V_{gs} -V_o) \\ KCL: I_{gd} &= g_mV_{gs} + \frac{V_o}{R_L’} +sC_LV_o \\ 结合以上三式:\frac{V_o}{V_{sig}} &= \frac{sC_{gd} - g_m}{\frac{1}{R_L’} + sC_L + sC_{gd}} \\ &= -g_mR_L’ \frac{1 - s(C_{gd}/g_m)}{1 + sR_L’(C_L + C_{gd})} \\\ \\ \therefore f_Z &= \frac{g_m}{2\pi C_{gd}} \\ 3-dB \ Frequency \ f_H &= \frac{1}{2\pi (C_L + C_{gd}) R_L’} \\ \frac{f_Z}{f_H}&= g_mR_L’ (1 + \frac{C_L}{C_{gd}}) \\ f_t &= |A_M|f_H \\ &= g_mR_L’ f_H \\ &= \frac{g_m}{2\pi (C_L + C_{gd})} \end{aligned} $$

3. Frequency Response

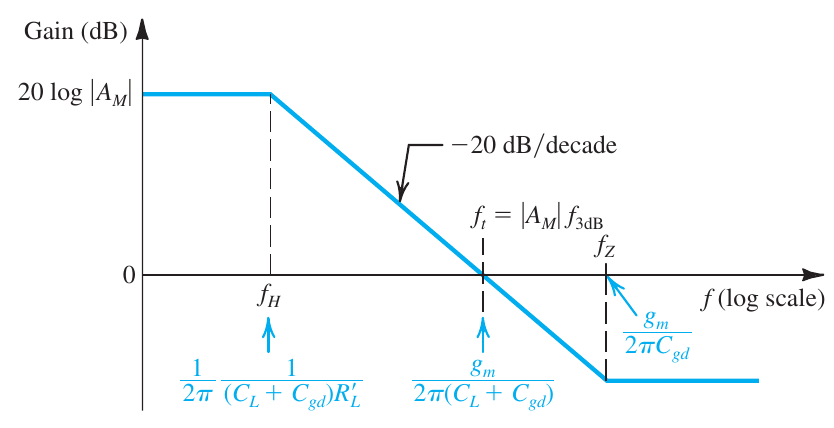
总结

$$ \begin{aligned} C_{in} &= C_{gs} + C_{gd}(1 + g_mR_L’) \\ &= C_{gs} + C_{eq} \\ R_{sig}’ &= R_{sig} || R_G \\ &\approx R_{sig} \\ \therefore 当 &R_{sig}很大时, f_H会被低估 \end{aligned} $$

Miller’s Theorem

米勒等效电路

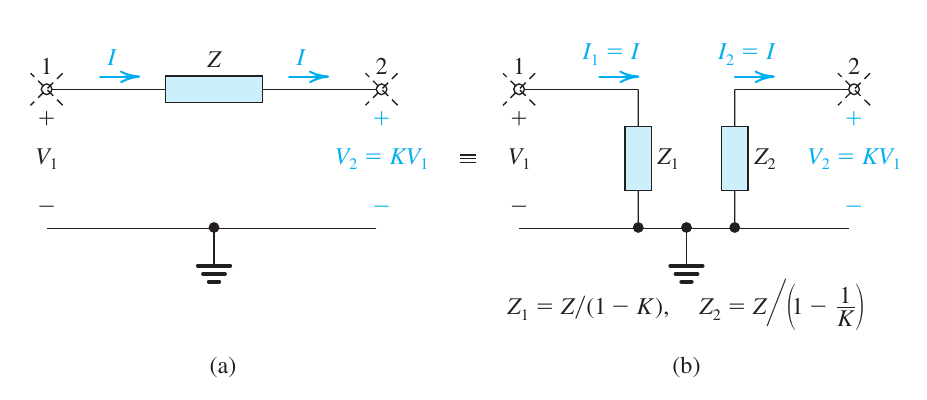
拆分阻抗

$$ \begin{aligned} V_2 & = KV_1 \\ Z &= Z_1 + Z_2 \\ 令Z_1 &= \frac{Z}{1-K} ,Z_2 = \frac{Z}{1 - \frac{1}{K}} \\ 使得I_1 &= I_2 = I \end{aligned} $$

Feedback

The General Feedback Structure

图示

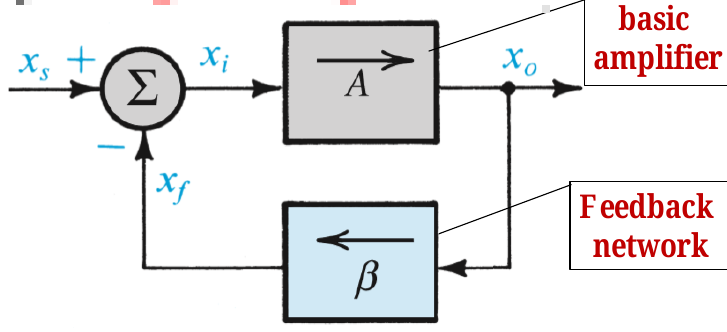
• $x$代表电压或者电流信号

分析

• $\beta$: Feedback Factor

$$ \begin{aligned} x_o &= Ax_i \\ x_f &= \beta x_o \\ x_i&= x_s - x_f \\ A_f &\equiv \frac{x_o}{x_s} \\ &= \frac{Ax_i}{x_f + x_i} \\ &= \frac{Ax_i}{x_i + \beta x_o} \\ &= \frac{Ax_i}{x_i + A\beta x_i} \\ &= \frac{A}{1 + A\beta} \\ &\approx \frac{1}{\beta} (A\beta \gg 1, 即\beta \gg \frac{1}{A}) \\\ \\ x_f &= \beta x_o =\frac{A\beta}{1 + A\beta}x_s \\ x_i &= x_s - x_f =\frac{1}{1 + A\beta}x_s \end{aligned} $$

• $A\beta$: Loop Gain

• $1 + A\beta$: The amount of Feedback

公式总结

$$ \begin{aligned} A_f &= \frac{A}{1 + A\beta} = (\frac{1}{\beta})\frac{1}{ 1 + 1/(A\beta)}\\ x_f &= \frac{A\beta}{1 + A\beta} x_s \\ x_i &= \frac{1}{1 + A\beta}x_s \\\ \\ 当A\beta &\gg 1: \\ A_f &\approx \frac{1}{\beta} \\ x_o &\approx x_s \\ x_f &\approx x_s \\ x_i &\approx 0 \\ 输入几乎&为0, 信号与反馈几乎抵消 \end{aligned} $$

Properties

Gain Desensitivity

$$ \begin{aligned} A_f &= \frac{A}{1 + A\beta} \\ \frac{dA_f}{dA} &= \frac{1}{(1 + A\beta)^2} \\ dA_f &= \frac{A}{1 +A\beta} \frac{1}{(1 + A\beta)A}dA \\ \frac{dA_f}{A_f} &= \frac{1}{1 + A\beta}\frac{dA}{A} \end{aligned} $$

• $A_f$变化的幅度比$A$小

• 因此, $1 + A\beta$ 也叫Desensitivity Factor

Bandwidth Extension*

$$ \begin{aligned} A(s) &= \frac{A_M}{1 + s/\omega_H} \\ A_f &= \frac{A(s)}{1 + A(s) \beta} \\ &= \frac{A_M/(1+A_M\beta)}{1 + s/[(1 + A_M\beta)\omega_H]} \\ &= \frac{A_{fM}}{1 + s/(1 + A_M\beta)} \\ \omega_{Hf} &= (1+A_M\beta) \omega_H \\ \omega_{Lf} &= \frac{\omega_L}{1 + A_M\beta} \end{aligned} $$

Interference Reduction

1. Signal-to-Interference Ratio

$$ S/I = V_s / V_n $$

2. 图示

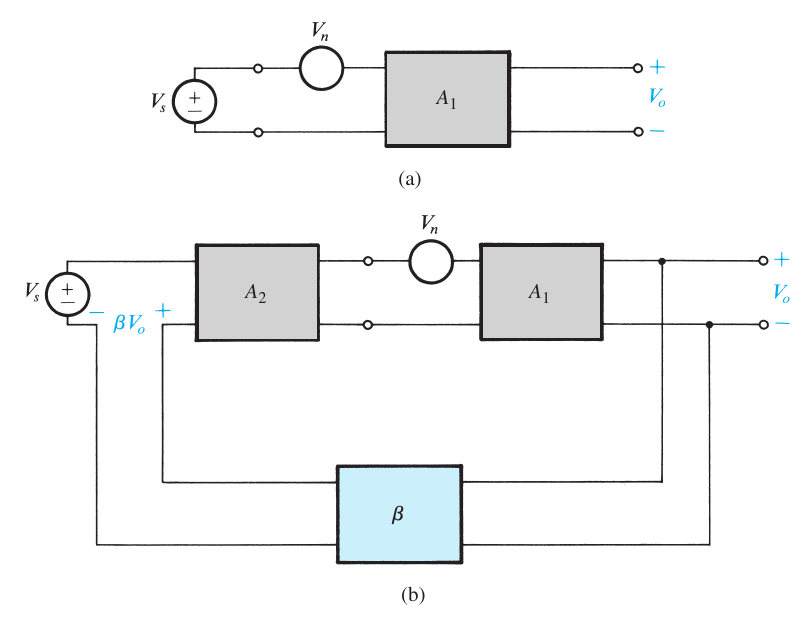
3. 分析

$$ \begin{aligned} V_o &= V_n \frac{A_1}{1 + A_1 A_2 \beta} + V_s \frac{A_1A_2}{1 + A_1A_2 \beta} \\ \therefore \frac{S}{I} &= \frac{V_s}{V_n}A_2 \end{aligned} $$

Reduction in Nonlinear Distortion

• Negative feedback may facilitate linearization

The Feedback Voltage Amplifier (Series-Shunt)

Basic Structure

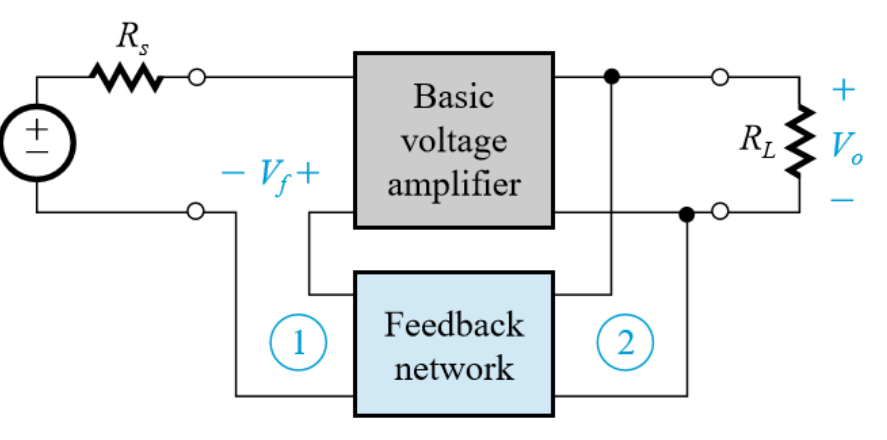
The Series–Shunt Feedback Topology

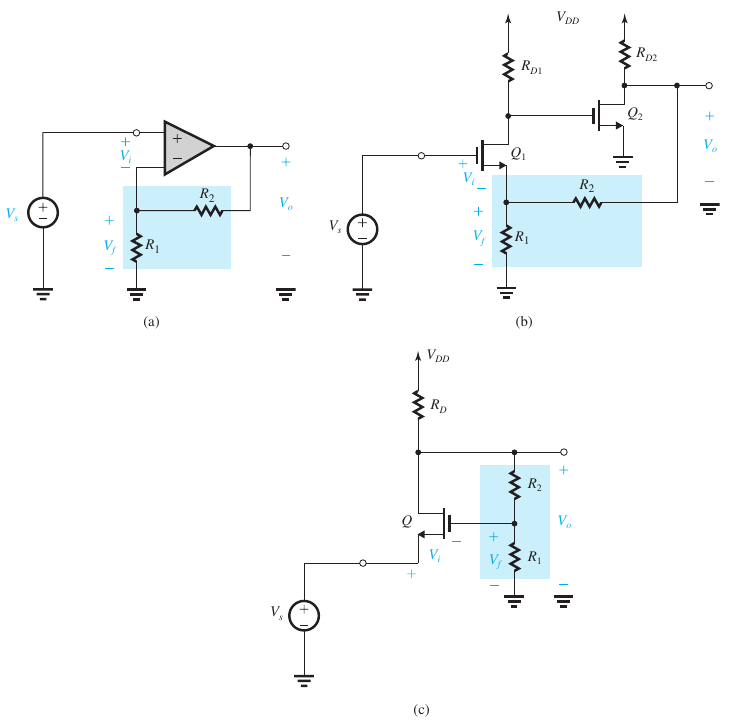
Systematic Analysis of Feedback Voltage Amplifiers

电路

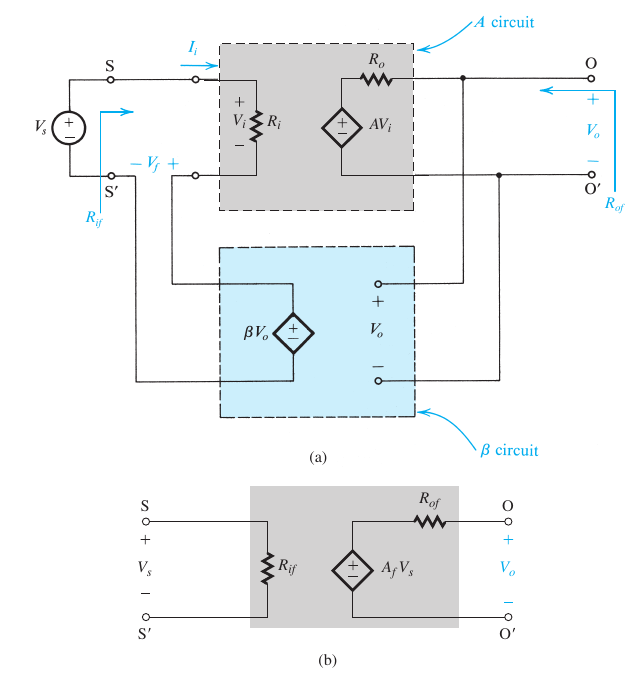
分析1

$$ \begin{aligned} V_i &= \frac{V_s}{1 + A\beta} \\ \therefore I_i &= \frac{V_s}{(1 +A\beta)R_i} \\ R_{if} &= \frac{V_s}{I_i} \\ &=(1 +A\beta) R_i \\\ \end{aligned} $$

分析2

1. 图示

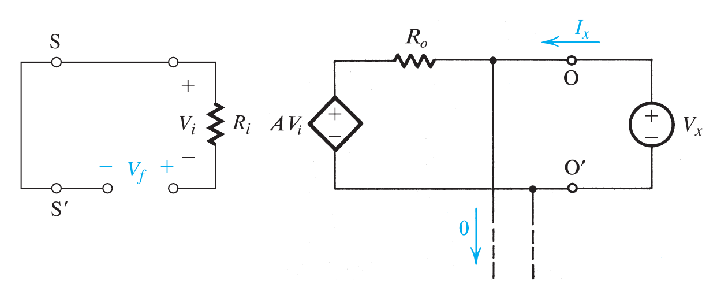
2. 数学分析

$$ \begin{aligned} 令V_s &= 0, 对输出端施加测试电压V_X = V_o \\ R_{of} &= \frac{V_X}{I_X} \\ I_X &= \frac{V_X - AV_i}{R_o} \\ \because V_s &=0 \\ \therefore V_i &= - V_f = -\beta V_o = -\beta V_X\\ \therefore I_X &= \frac{V_X(1 + A\beta)}{R_o} \\ \therefore R_{of} &= \frac{R_o}{1 + A\beta} \end{aligned} $$

A Practical Case

1. 电路

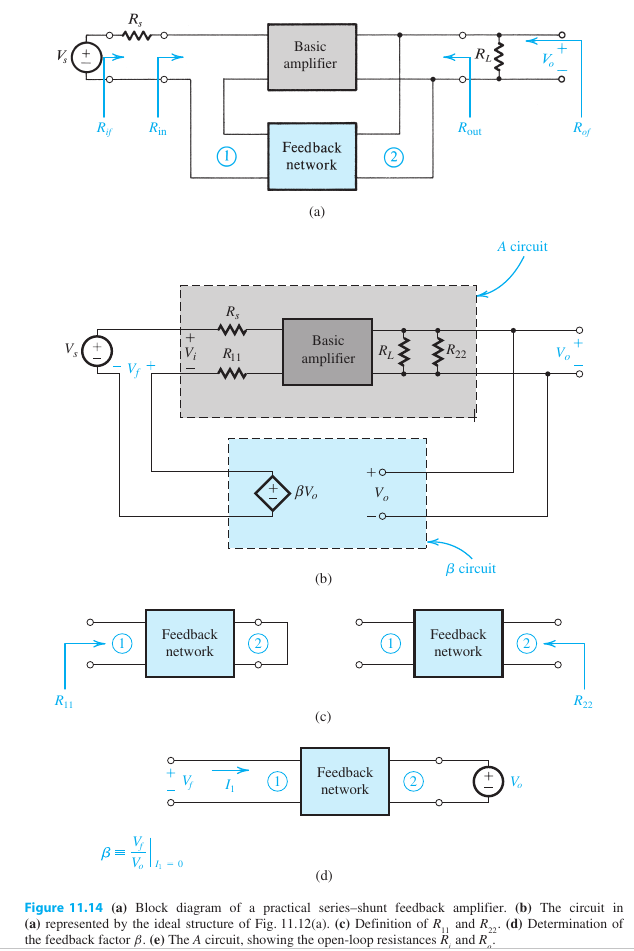
2. 分析

$$ \begin{aligned} \beta &\equiv \frac{V_f}{V_o} \\ A_f &\equiv \frac{V_o}{V_s} \\ &= \frac{A}{1 + A\beta} \\ R_{if} &= R_i(1 + A\beta) \\ R_{of} &= R_o/(1 + A\beta) \\ R_{in} &= R_{if} - R_s \\ R_{out} &= 1/(\frac{1}{R_{out}} - \frac{1}{R_L}) \end{aligned} $$

Other Feedback-Amplifier Types

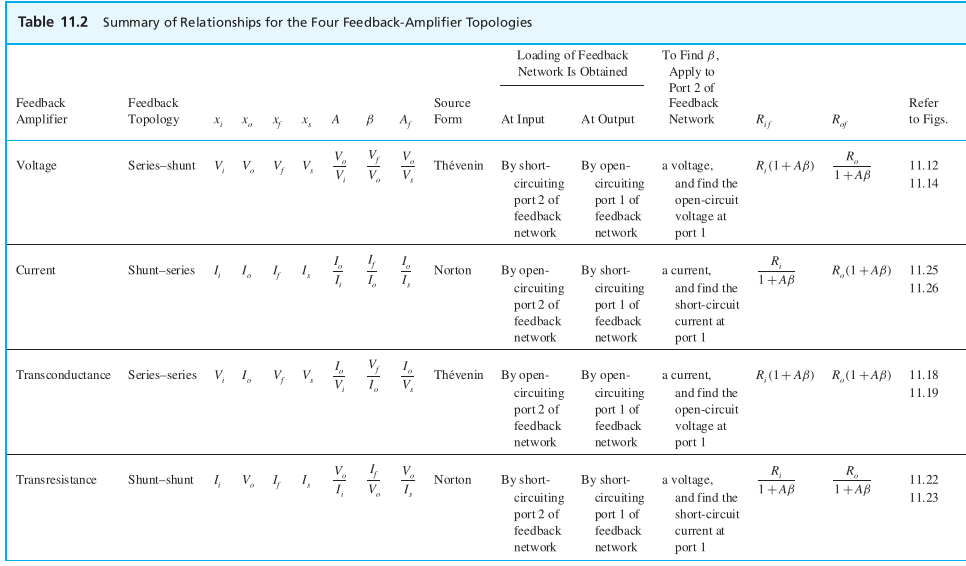
The Feedback Transconductance Amplifier (Series–Serie)

理想电路

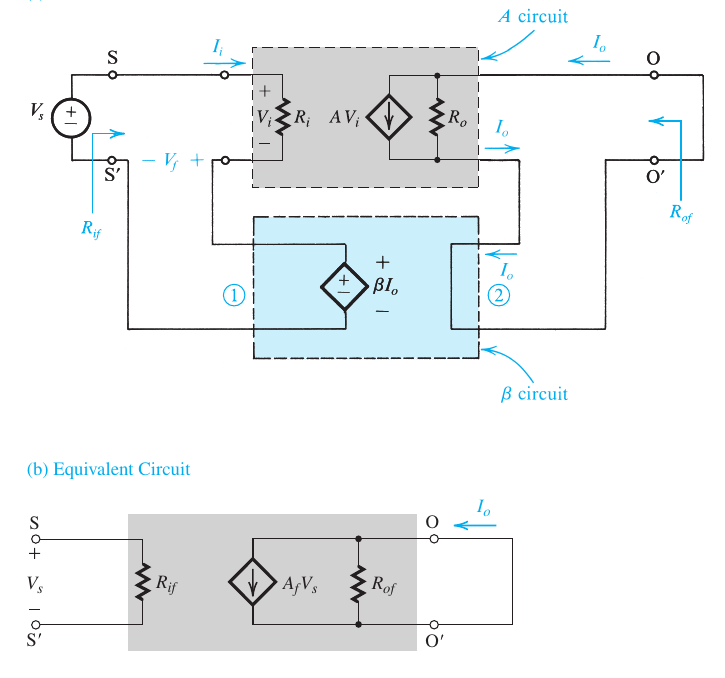
• 反馈网络对原网络没有负载效应

• 输出是什么，就稳什么

公式

$$ \begin{aligned} A_f &\equiv \frac{I_o}{V_i} = \frac{A}{1 + A\beta} \\ R_{if} &= (1 + A\beta) R_i \\ R_{of} &= (1 + A\beta ) R_o \\ R_{in} &= R_{if} - R_s \\ R_{out}&= R_{of} - R_L \\ \end{aligned} $$

The Feedback Transresistance Amplifier (Shunt–Shunt)

电路

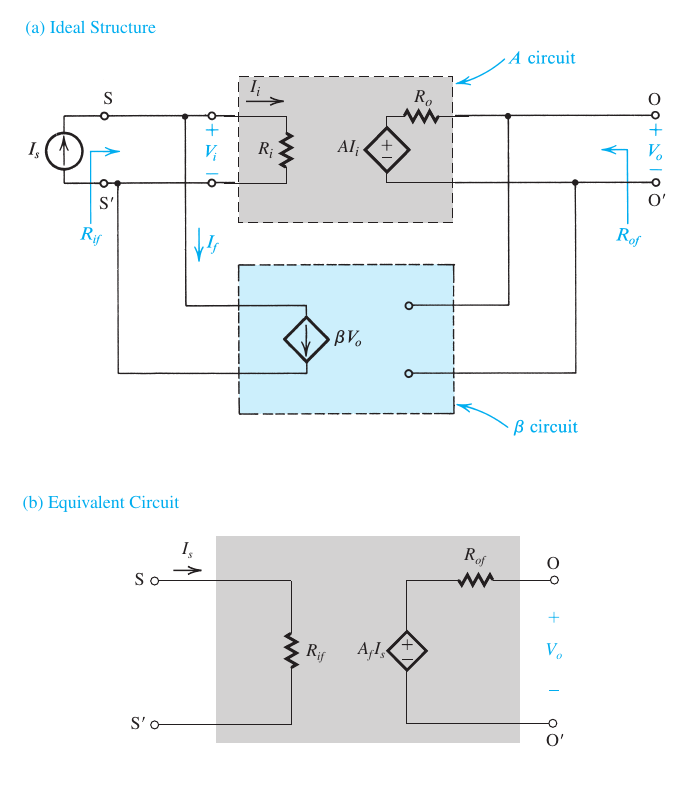
公式

$$ \begin{aligned} A &\equiv \end{aligned} $$

附录

Bypass Capacitor

过滤高频噪声，以确保电路中的稳定电压

Coupling Capacitor

放置在信号线上，用于将一个信号传输到另一个电路中，同时阻止直流偏移。

dominant pole

最高极点频率的极点。这个极点对于电路的频率响应和稳定性非常重要。

Zero Frequency

a transmission zero is the value of s at which the input does not reach the output, resulting in $V_o = 0$

$f_L$公式推导

$$ 这个公式是基于滤波器的频率响应推导出来的。\\ \\ 假设有一个由三个电感（inductors）和三个电容（capacitors）组成的低通滤波器（low-pass filter），其中电感之间互相并联，电容之间也互相并联。这个滤波器的频率响应可以表示为：\\ \\ H(f) = \frac{1}{1+j\frac{f}{f_{P1}}} \cdot \frac{1}{1+j\frac{f}{f_{P2}}} \cdot \frac{1}{1+j\frac{f}{f_{P3}}}\\ \\ 其中，f是频率，f_P1、f_P2和f_P3是分别由电容和电感决定的三个截止频率（cut-off frequency），式子中的j是虚数单位，满足j^2=-1。\\ \\ 将H(f)表示成模与相位的形式，可以得到：\\ \\ H(f) = \frac{A}{\sqrt{1+(\frac{f}{f_{P1}})^2} \cdot \sqrt{1+(\frac{f}{f_{P2}})^2} \cdot \sqrt{1+(\frac{f}{f_{P3}})^2}} \cdot e^{-j\phi(f)}\\ \\ 其中，A和φ(f)分别是幅度和相位，可以通过求解每个因子的幅度和相位，再将它们相乘得到H(f)的幅度和相位。\\ \\ 令f_Z = \frac{1}{2\pi\sqrt{LC}}为电感和电容组成的谐振频率，其中L和C是电感和电容的值。假设f_Z^2远小于f_P1^2、f_P2^2和f_P3^2，可以将H(f)中的每个因子展开成泰勒级数，保留到二阶，得到：\\ \\ H(f) \approx \frac{A}{\sqrt{1+\frac{1}{4}(\frac{f}{f_Z})^2} \cdot \sqrt{1+\frac{1}{4}(\frac{f}{f_Z})^2} \cdot \sqrt{1+\frac{1}{4}(\frac{f}{f_Z})^2}} \cdot e^{-j\phi(f)}\\ \\ 将三个根号内的项视为一个整体，可以得到：\\ \\ H(f) \approx \frac{A}{(1+\frac{1}{4}(\frac{f}{f_Z})^2)^{\frac{3}{2}}} \cdot e^{-j\phi(f)}\\ \\ 对于一个低通滤波器，当f«f_P1、f_P2和f_P3时，H(f)的幅度近似为1，相位近似为0。因此，可以将H(f)中的A近似为1，φ(f)近似为0，得到：\\ \\ H(f) \approx \frac{1}{(1+\frac{1}{4}(\frac{f}{f_Z})^2)^{\frac{3}{2}}}\\ \\ 将H(f)的幅度与相位分别表示成模和复数的形式，可以得到：\\ \\ |H(f)| = \frac{1}{\sqrt{1+\frac{1}{16}(\frac{f}{f_Z})^4}}\\ \\ 将|H(f)|表示成f的函数，并令其等于0.707，可以解出f_L，得到：\\ \\ f_L \approx \sqrt{f_{P1}^2 + f_{P2}^2 + f_{P3}^2 - 2f_Z^2}\\ $$

电容的阻抗

• 电容通常很小,$1/sC$也就很大，通常可以忽略不计

$R_{if} 和 R_i$

$$ \begin{aligned} R_{if} &= \frac{\pmb {V_s}}{I_i} \\ R_i &= \frac{\pmb {V_i}}{I_i} \end{aligned} $$

增益与中段增益

$A(s) = \frac{A_M}{1 + s/\omega_H}$

这个传输函数可以通过对电路进行拉普拉斯变换得到。假设我们有一个电路，其中输入信号为 $V_{in}(t)$，输出信号为 $V_{out}(t)$。我们可以将电路表示为一个线性常微分方程：

$$ L\frac{dV_{out}(t)}{dt} + R V_{out}(t) = V_{in}(t) $$

其中 $L$ 和 $R$ 分别是电感和电阻的值。应用拉普拉斯变换，我们得到：

$$ LsV_{out}(s) + RV_{out}(s) = V_{in}(s) $$

将 $V_{out}(s)$ 移项并合并同类项，得到：

$$ \frac{V_{out}(s)}{V_{in}(s)} = \frac{1}{Ls + R} $$

这个比值即电路的传输函数，表示了输入信号和输出信号之间的关系。

接下来，我们可以将传输函数改写为标准的一阶低通滤波器的形式。首先，我们可以将传输函数的分母写成 $1 + s/\omega_H$ 的形式，其中 $\omega_H = R/L$ 是电路的截止频率。这是因为当 $s = j\omega$ 时，分母变为 $1 + j\omega/\omega_H$，其模长为 $\sqrt{1 + (\omega/\omega_H)^2}$，当 $\omega \ll \omega_H$ 时，模长近似为 $1$，而当 $\omega \gg \omega_H$ 时，模长近似为 $\omega/\omega_H$，表示信号被滤波器削弱的程度。

为了把传输函数写成标准形式，我们可以将分子和分母同时除以 $A_M$，得到：

$$ A(s) = \frac{A_M/L}{s/\omega_H + 1} = \frac{A_M}{1 + s/\omega_H} $$

这个形式与标准的一阶低通滤波器的传输函数形式一致，其中 $A_M/L$ 是增益常数，$1/\omega_H$ 是电路的时间常数，表示电路对输入信号的响应速度。

拉普拉斯变换

定义

给定一个函数 $f(t)$，它的拉普拉斯变换 $F(s)$ 定义为：

$$F(s) = \mathcal{L}{f(t)} = \int_{0}^{\infty} e^{-st} f(t) dt $$

其中 $s$ 是复变量，$e^{-st}$ 是一个复指数函数，$f(t)$ 是一个定义在非负实数域上的函数。这个积分表示了在复平面上以直线 $Re(s) = \sigma$ 为边界的区域内，$F(s)$ 的积分值。

性质

1. 线性性，即对于任意常数 $a$ 和 $b$，有：

$$ \mathcal{L}{a f(t) + b g(t)} = a F(s) + b G(s) $$

其中 $f(t)$ 和 $g(t)$ 是两个函数，$F(s)$ 和 $G(s)$ 是它们的拉普拉斯变换。

2. 微分和积分定理

如果 $f(t)$ 有一个连续的导数 $f’(t)$，那么它的拉普拉斯变换为：

$$ \mathcal{L}{f’(t)} = sF(s) - f(0) $$

其中 $f(0)$ 是 $f(t)$ 在 $t=0$ 处的值。类似地，如果 $f(t)$ 是一个连续函数，并且存在一个常数 $T$，使得 $f(t) = 0$ 对于所有 $t < 0$ 和 $t > T$ 成立，那么它的拉普拉斯变换为：

$$ \mathcal{L}{\int_0^t f(\tau)d\tau} = \frac{F(s)}{s} $$