Basic Concepts
常用概念
| 名称 | 概念 |
|---|---|
| Wavelength | $\lambda = \dfrac{ 1 }{ f \sqrt{ \epsilon \mu } } = \dfrac{ c }{ f \sqrt{ \mu_r \epsilon_r } }$ |
| Phase Velocity | $v_p = f \lambda = \dfrac{ \omega }{ \beta } = \dfrac{ c }{ \sqrt{\varepsilon_r \mu_r }}, f = \sqrt{ \varepsilon_r} f_0$ |
| Phase Shift | $\phi = 2 \pi \dfrac{ l }{ \lambda }$ |
| Normalized Frequency | $f_N =$ |
| 常见频率波长转换 | $2.4GHz \longleftrightarrow \lambda= 12.5cm \ 5GHz \longleftrightarrow \lambda = 6cm \ 10GHz \longleftrightarrow \lambda = 3cm$ |
频谱划分 & 无线通信系统的工作频率
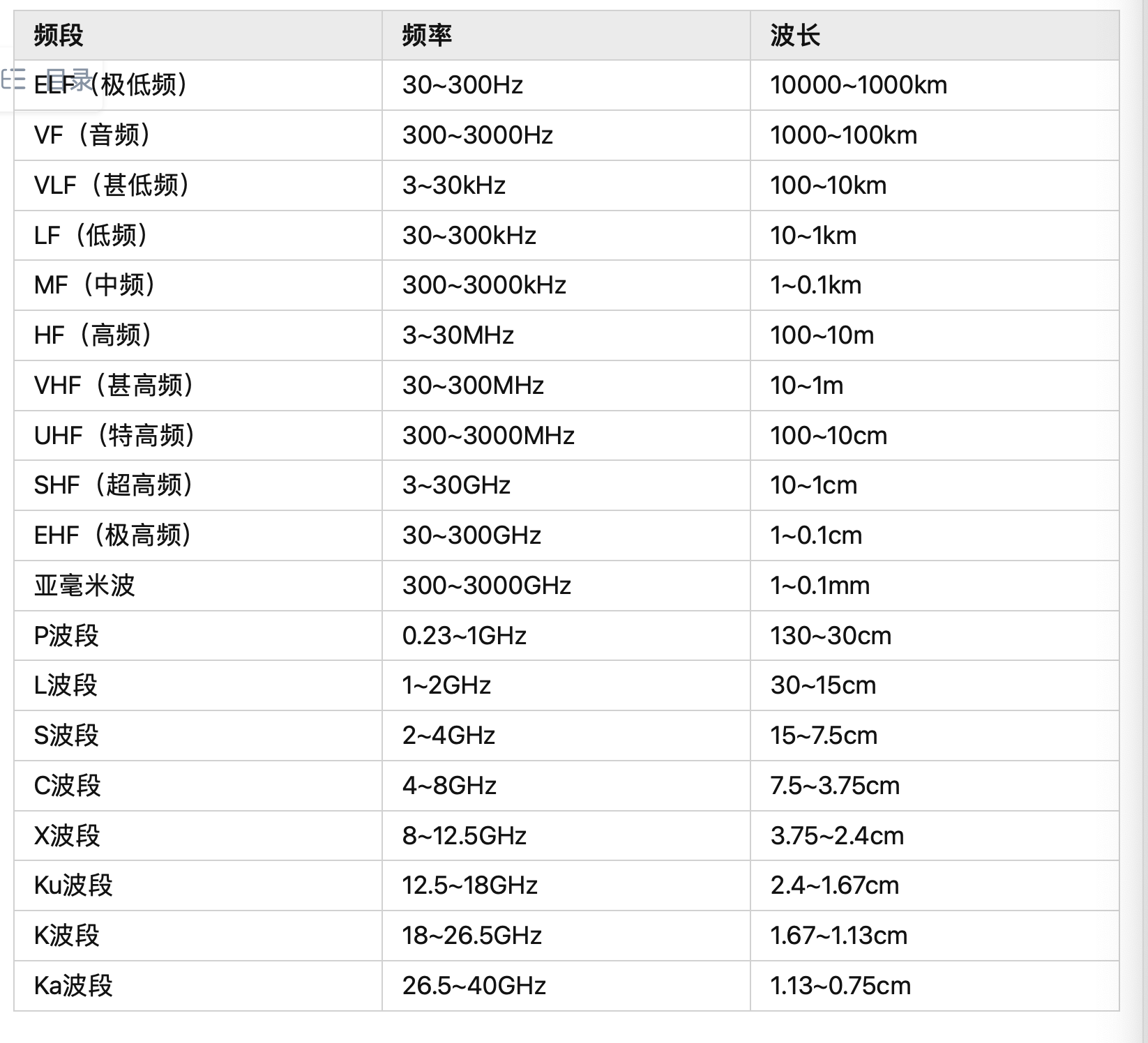
| 名称 | 范围 |
|---|---|
| W | 75GHz - 110GHzq |
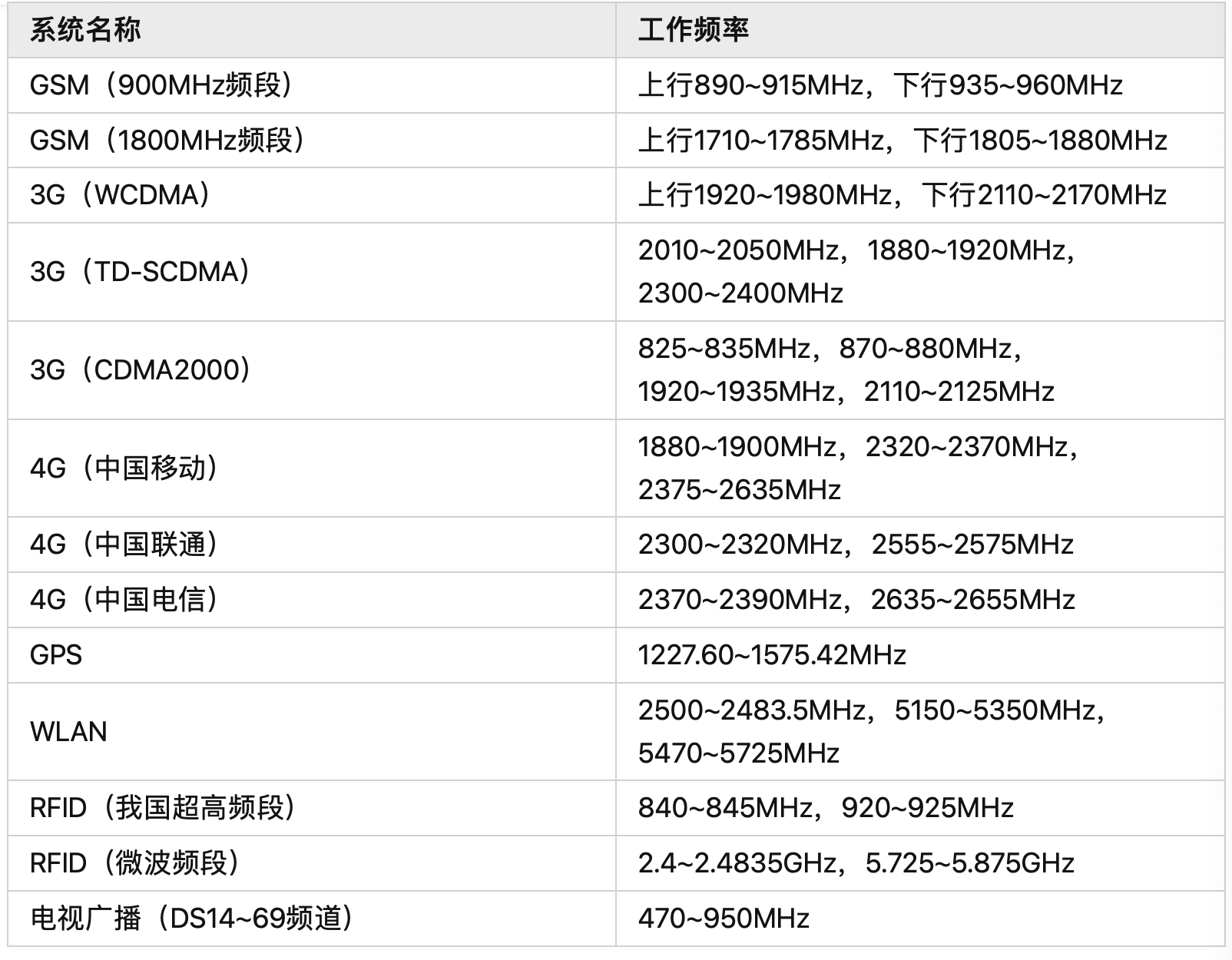
Radio Frequency & Microwave
| 分类 | Radio Frequency | Microwave |
|---|---|---|
| 频率 | $30MHz - 100GHz+$ | $300MHz - 3000GHz$ |
| 优点 | 速度快,频率高,带宽大,尺寸小 | |
| 缺点 | 成本高,功率小,辐射损耗大 |
The Lumped-Element Circuit Model for a Transmission Line
Telegrapher’s Equation
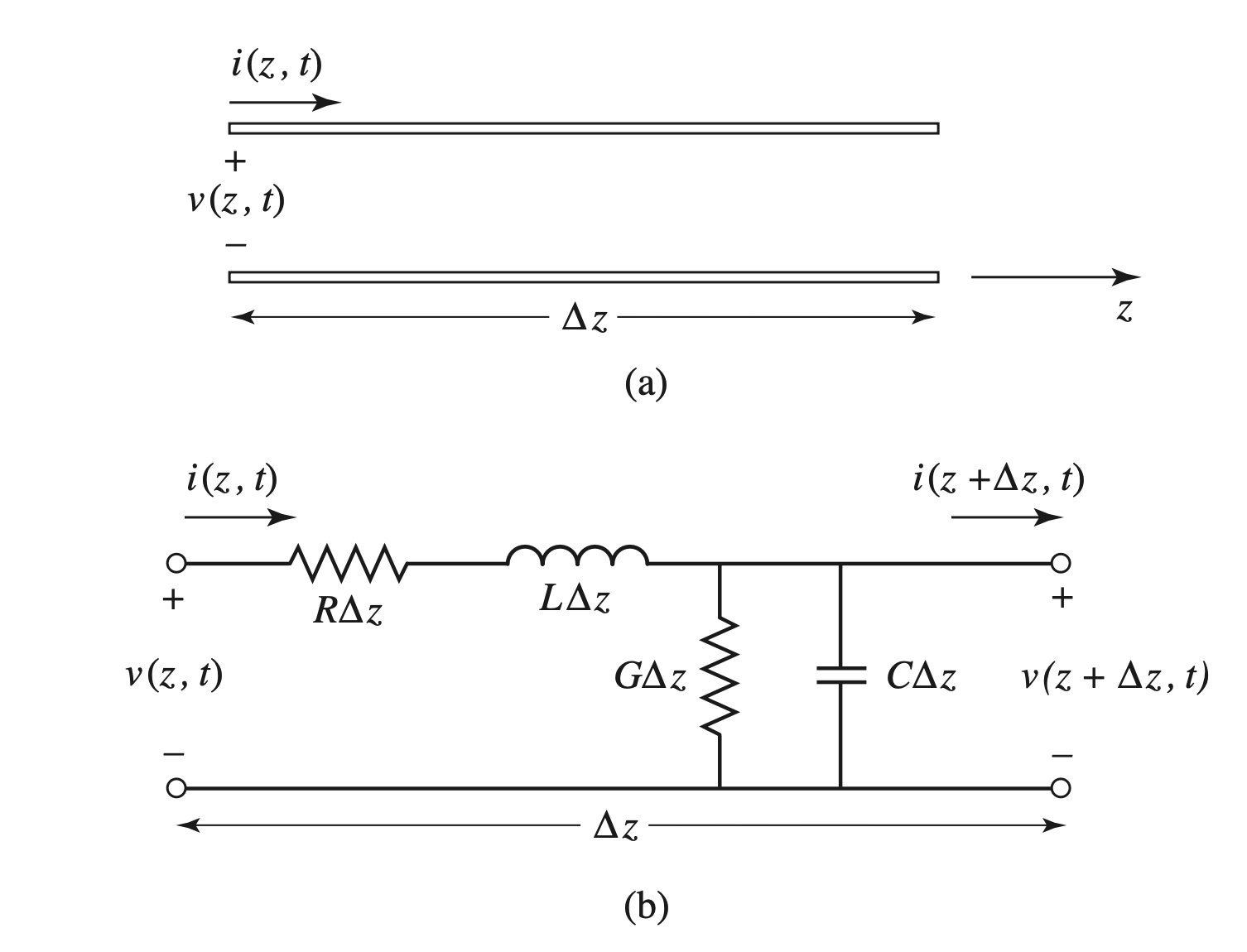
$$ \begin{aligned} v(z,t) - v(z + \Delta z, t) - i(z,t) R \Delta z - L \Delta z\frac{ \partial i(z,t) }{ \partial t } &= 0 \\ i(z,t) - i(z + \Delta z, t) - G \Delta z \cdot v(z + \Delta z,t) - C \Delta z \frac{ \partial v(z + \Delta z, t) }{ \partial t } &= 0 \end{aligned} $$
- 将以上式子同时除以$\Delta z$, 得到Telegrapher’s Equation
$$ \begin{gather} \begin{aligned} \frac{ \partial V(z,t) }{ \partial z } &= - Ri (z,t) - L \frac{ \partial i(z,t) }{ \partial t } \\ \frac{ \partial i(z,t) }{ \partial z } &= - GV (z,t) - C \frac{ \partial V(z,t) }{ \partial t } \end{aligned} \end{gather} $$
- 频域下的Telegrapher’s Equation
$$ \begin{gather} \begin{aligned} \frac{ dV(z) }{ dt } &= - (R + j \omega L) I(z) \\ \frac{ dI(z) }{ dt } &= - (G + j \omega C) V(z) \end{aligned} \end{gather} $$
Wave Propagation on Transmission
- Wave Equations
$$ \begin{gather} \begin{aligned} \frac{ d^2 V(z) }{ dz^2 } &= - \gamma^2 V(z) \\ \frac{ d^2 I(z) }{ dz^2 } &= - \gamma^2 I(z) \\ \gamma &= \sqrt{ (R + j \omega L) ( G + j \omega C) } = \alpha + j \beta \end{aligned} \end{gather} $$
- Solutions
- Not Considering Time
$$ \begin{gather} \begin{aligned} V(z) &= V_0^+ e^{- \gamma z} + V_0^- e^{ \gamma z} \\ I(z) &= I_0^+ e^{- \gamma z} + I_0^- e^{ \gamma z} \\ &= \frac{ \gamma }{ R + j \omega L } (V_0^+ e^{- \gamma z} - V_0^- e^{ \gamma z}) \\ &= \frac{ V_0^+ }{ Z_0 } e^{ - \gamma z} - \frac{ V_0^- }{ Z_0 }e^{ \gamma z} \end{aligned} \end{gather} $$
- In Time Domain
$$ \begin{gather} \begin{aligned} v(z,t) &= |V_0^+| cos( \omega t - \beta z + \phi^+) e^{- \alpha z} + |V_0^-| cos( \omega t - \beta z + \phi^-) e^{\alpha z} \\ V_0^+ &= |V_0^+| e^{j \phi^+}, V_0^- = |V_0^-| e^{j \phi^-} \end{aligned} \end{gather} $$
- Characteristic Impedance
$$ \begin{gather} \begin{aligned} Z_0 &= \sqrt{ \frac{ R + j \omega L }{ G + j \omega C } } \\ &= \frac{ V_0^+ }{ I_0^+} = - \frac{ V_0^- }{ I_0^- } \end{aligned} \end{gather} $$
Parameters for Lossless Lines
$$ \begin{gather} \begin{aligned} \alpha &= 0, \beta = \omega \sqrt{ LC } \\ Z_0 &= \sqrt{ \frac{ L }{ C } } \\ v_p &= \frac{ \omega }{ \beta } = \frac{ 1 }{ \sqrt{ LC } } \end{aligned} \end{gather} $$
Field Analysis for Transmission Lines …
Transmission Line Parameters
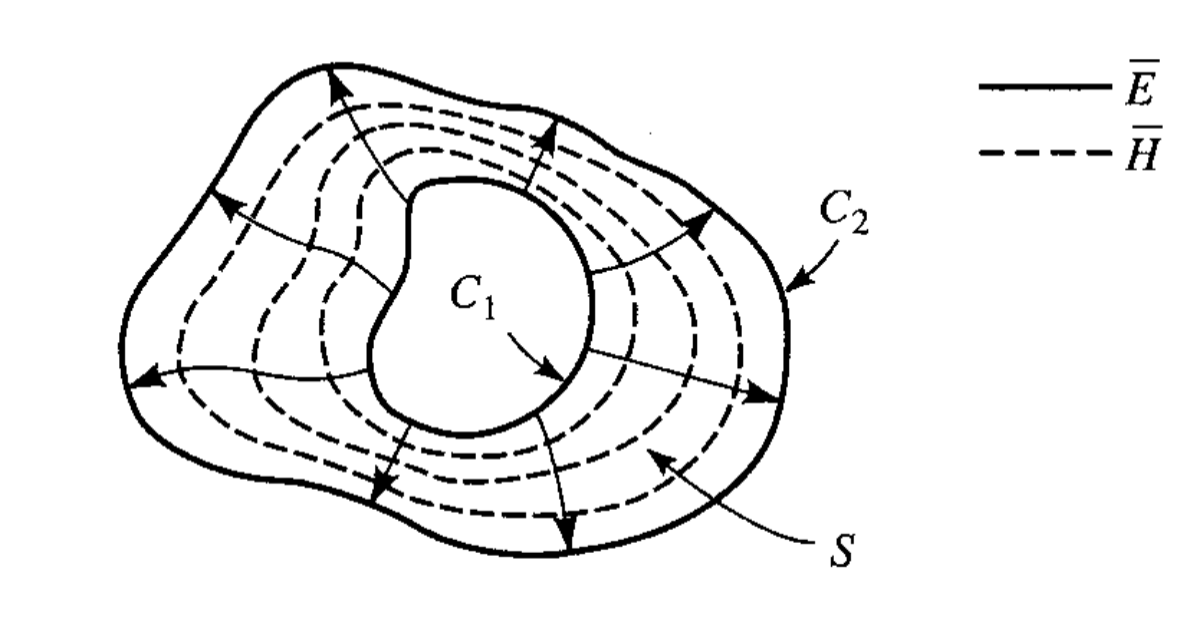
Inductors & Capacitors
$$ \begin{gather} \begin{aligned} W_m &= \frac{ \mu }{ 4 } \int_{ S }^{ } \overrightarrow{ H } \cdot \overrightarrow{ H }^* ds = \frac{ 1 }{ 4 } L |I_0|^2 \\ \therefore L &= \frac{ \mu }{ |I_0|^2 } \int_{ S }^{ } \overrightarrow{ H } \cdot \overrightarrow{ H }^* ds (H/m)\\ C &= \frac{ \epsilon }{ |V_0|^2 } \int_{ S }^{ } \overrightarrow{ E } \cdot \overrightarrow{ E }^* ds (F/m) \end{aligned} \end{gather} $$
Lossy Energy Per Unit Length
$$ \begin{gather} \begin{aligned} P_c &= \frac{ R_s }{ 2 } \int_{ C_1 + C_2 }^{ } \overrightarrow{ H } \cdot \overrightarrow{ H }^* dl = \frac{ 1 }{ 2 } |I_0|^2 R \\ \therefore R &= \frac{ R_s }{ |I_0|^2} \int_{ C_1 + C_2 }^{ } \overrightarrow{ H } \cdot \overrightarrow{ H }^* dl \\ P_d &= \frac{ \omega \epsilon’’ }{ 2 } \int_{ S }^{ } \overrightarrow{ E } \cdot \overrightarrow{ E }^* ds = \frac{ 1 }{ 2 } G |V_0|^2 \\ \therefore G &= \frac{ \omega \epsilon’’ }{ |V_o|^2 } \int_{ S }^{ } \overrightarrow{ E } \cdot \overrightarrow{ E }^* ds (S/m) \end{aligned} \end{gather} $$
Transmission Line Parameters for Some Common Lines
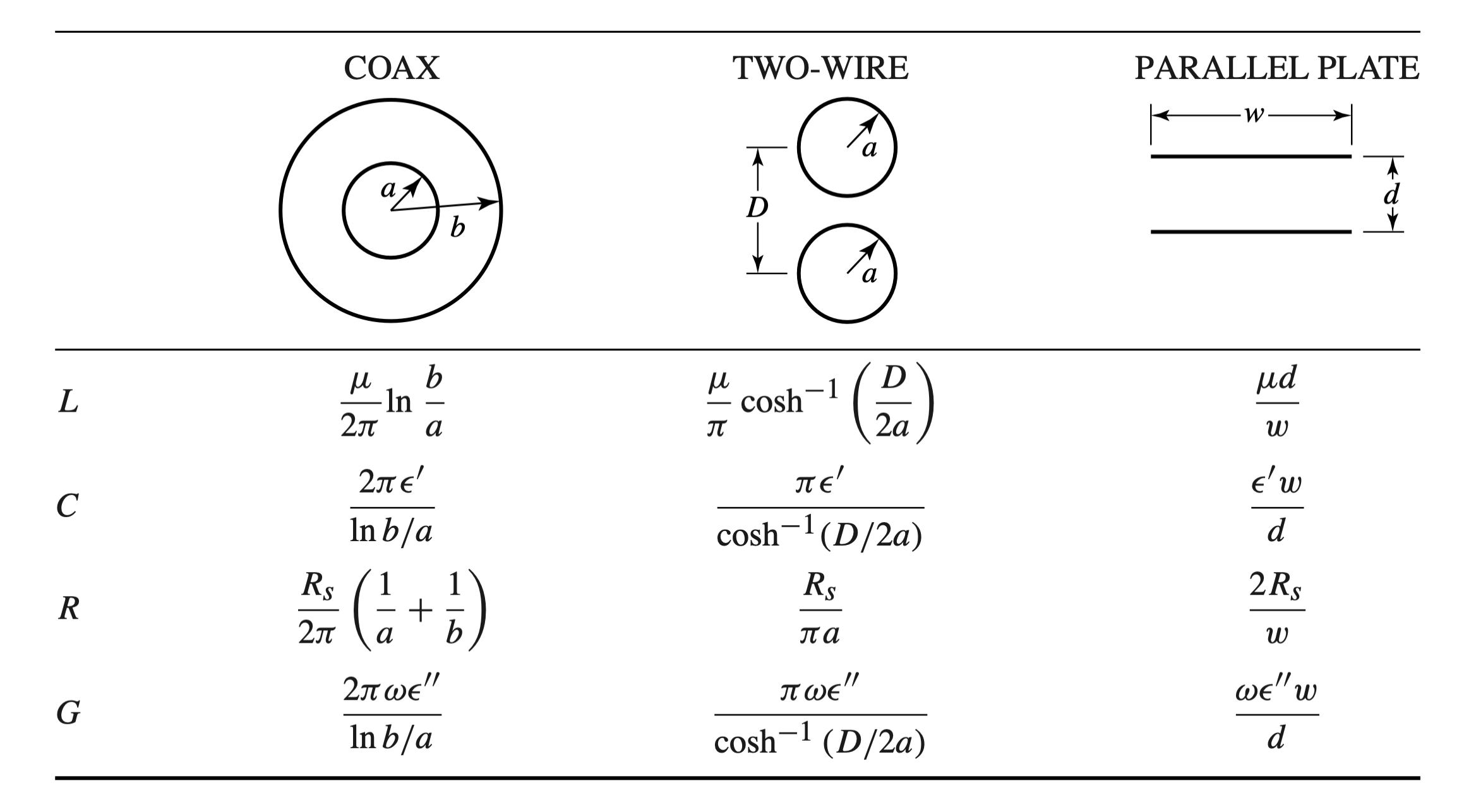
Terminated Lossless Transmission Line
Impedances & Reflection Coefficient
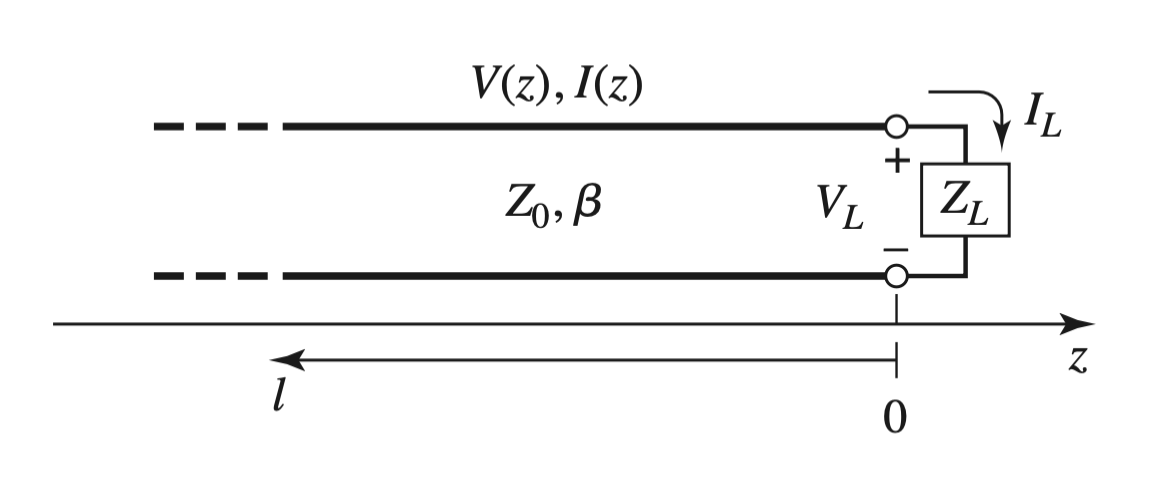
Input / Load Impedances
- Reflection Coefficient & Transimission Coefficient
$$ \begin{gather} \begin{aligned} \Gamma &= \frac{ V_0^- }{ V_0^+ } \\ &= \frac{ Z_L - Z_0 }{ Z_L + Z_0 } \\ &= | \Gamma| e^{ j \theta} \\ \Gamma(l) &= \Gamma e^{- 2j \beta l} \end{aligned} \end{gather} $$ 2. Transmission Line Impedance Equation
$$ \begin{gather} \begin{aligned} Z_L &= \frac{ V(0) }{ I(0) } \\ &= \frac{ V_0^+ + V_0^- }{ V_0^+ - V_0^- } Z_0 \\ Z_{in} &= \frac{ V(-l) }{ I(-l) } \\ &= \frac{ 1 + \Gamma e^{-2j \beta l} }{ 1 - \Gamma e^{-2 j \beta l} } Z_0 \\ &= Z_0 \frac{ Z_L + j Z_0 tan ( \beta l) }{ Z_0 + j Z_L tan ( \beta l) } \\ l &= -z \end{aligned} \end{gather} $$
- Voltage/Current Equations
$$ \begin{gather} \begin{aligned} V(z) &= V_0^+( e^{-j \beta z} + \Gamma e^{j \beta z}) \\ I(z) &= \frac{ V_0^+ }{ Z_0 }( e^{-j \beta z} - \Gamma e^{j \beta z}) \end{aligned} \end{gather} $$
Return/Insertion Loss & VSWR
- Return/Insertion Loss
$$ \begin{gather} \begin{aligned} RL &= -20 \cdot lg |\Gamma| dB \\ IL &= -20 \cdot lg |T| dB \end{aligned} \end{gather} $$
- Voltage Standing Wave Ratio
$$ \begin{aligned} |V(z)| &= |V_0^+| \cdot |1 + \Gamma e^{2j \beta z}| \\ &= |V_0^+| \cdot |1 + \Gamma e^{-2j \beta l}| \\ &= |V_0^+| \cdot (1 + | \Gamma| e^{j ( \theta - 2 \beta l)} \\ l &= -z \end{aligned} $$
$$ \begin{gather} \begin{aligned} VSWR &= \frac{ V_{max} }{ V_{min} } \\ &= \frac{ 1 + | \Gamma| }{ 1 - | \Gamma | } \end{aligned} \end{gather} $$
Special Cases
Short-Circuited
- $Z_L = 0, \Gamma = -1$
$$ \begin{gather} \begin{aligned} V(z) &= V_0^+(e^{-j \beta z} + e^{j \beta z}) \\ I(z) &= \frac{ V_0^+ }{ Z_0 } ( e^{-j \beta z} - e^{j \beta z}) \\ Z_{in} &= j Z_0 tan ( \beta l) \end{aligned} \end{gather} $$
Open-Circuited
$$ \begin{gather} \begin{aligned} Z_{in} &= -j Z_0 cot ( \beta l) \\ Z_{in} &= \begin{cases} Z_L & l = \dfrac{ \lambda }{ 2 } \\ \dfrac{ Z_0^2 }{ Z_L } & l = \dfrac{ \lambda }{ 4 } + n \dfrac{ \lambda }{ 2 } \end{cases} \end{aligned} \end{gather} $$
Feed/Load Lines
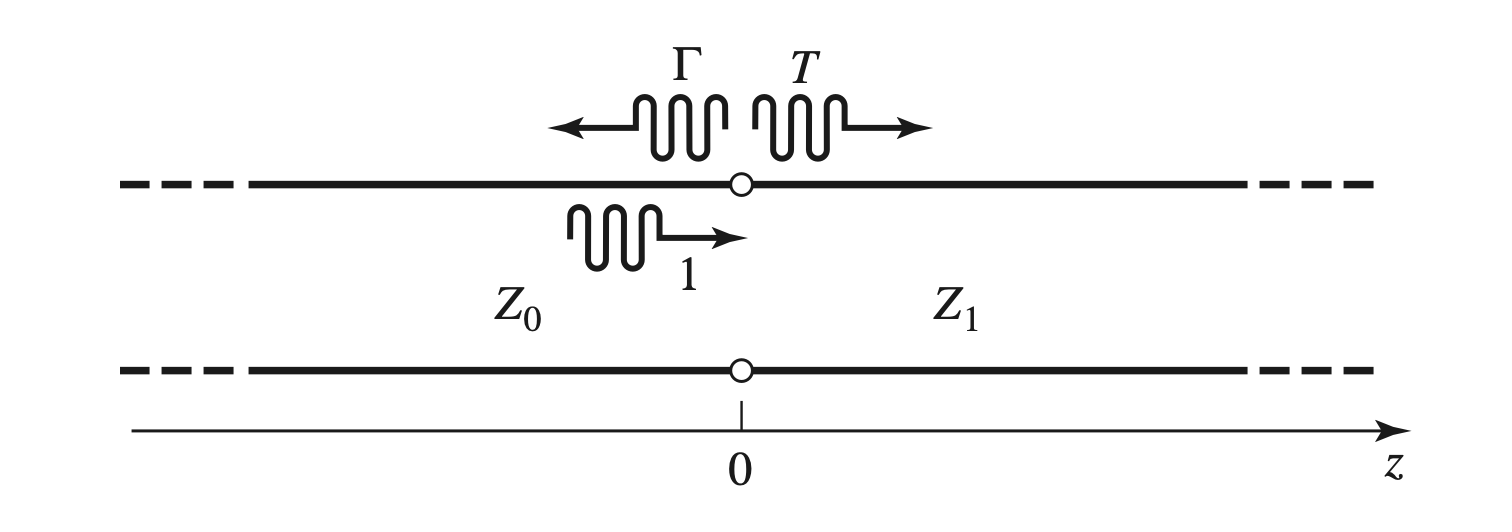
$$ \begin{gather} \begin{aligned} \Gamma &= \frac{ Z_1 - Z_0 }{ Z_1 + Z_0 } \\ T &= 1 + \Gamma \\ &= \frac{ 2Z_1 }{ Z_1 + Z_0 } \\ V(z) &= V_0^+ T e^{- j \beta z} , z > 0 \end{aligned} \end{gather} $$
Quarter-Wave Transformer
Impedance
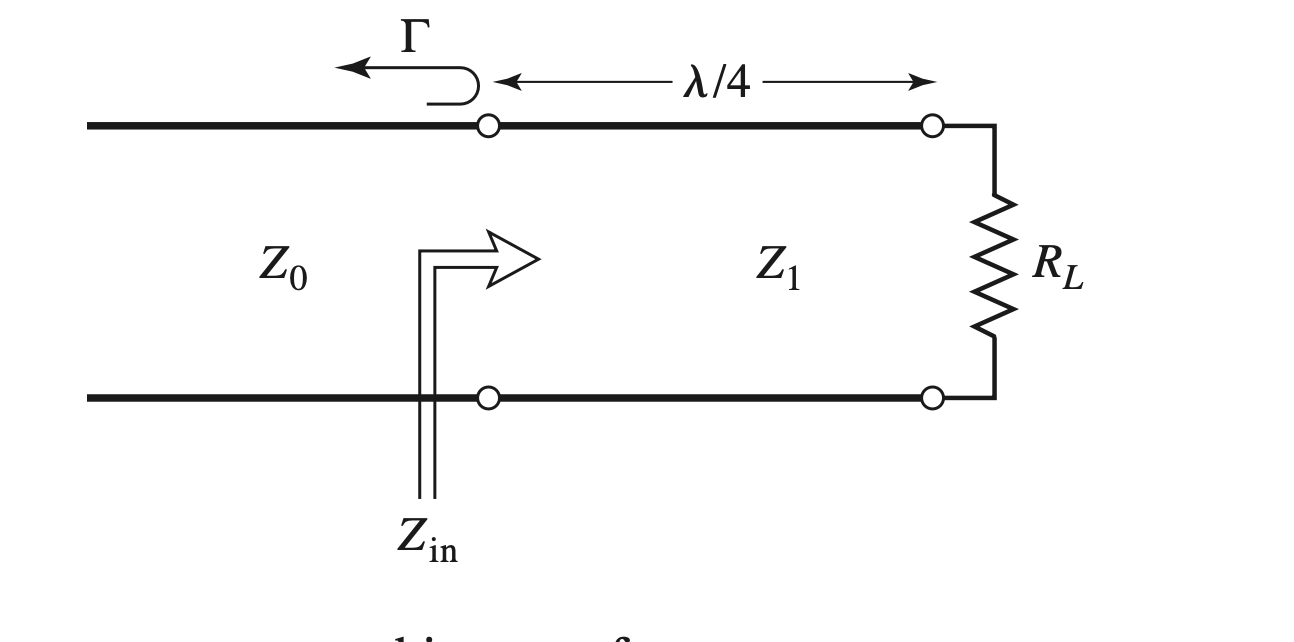
- 为了使得$\Gamma = 1$, $l = \dfrac{ \lambda }{ 4 }, Z_{in} = Z_0$
$$ \begin{gather} \begin{aligned} Z_{in} &= Z_1 \frac{ R_L + j Z_1 tan( \beta l) }{ Z_1 +j R_L tan( \beta l) } \\ &= \frac{ Z_1^2 }{ R_L } \\ Z_1 &= \sqrt{ Z_{0} R_L} \end{aligned} \end{gather} $$
Multiple-Reflection
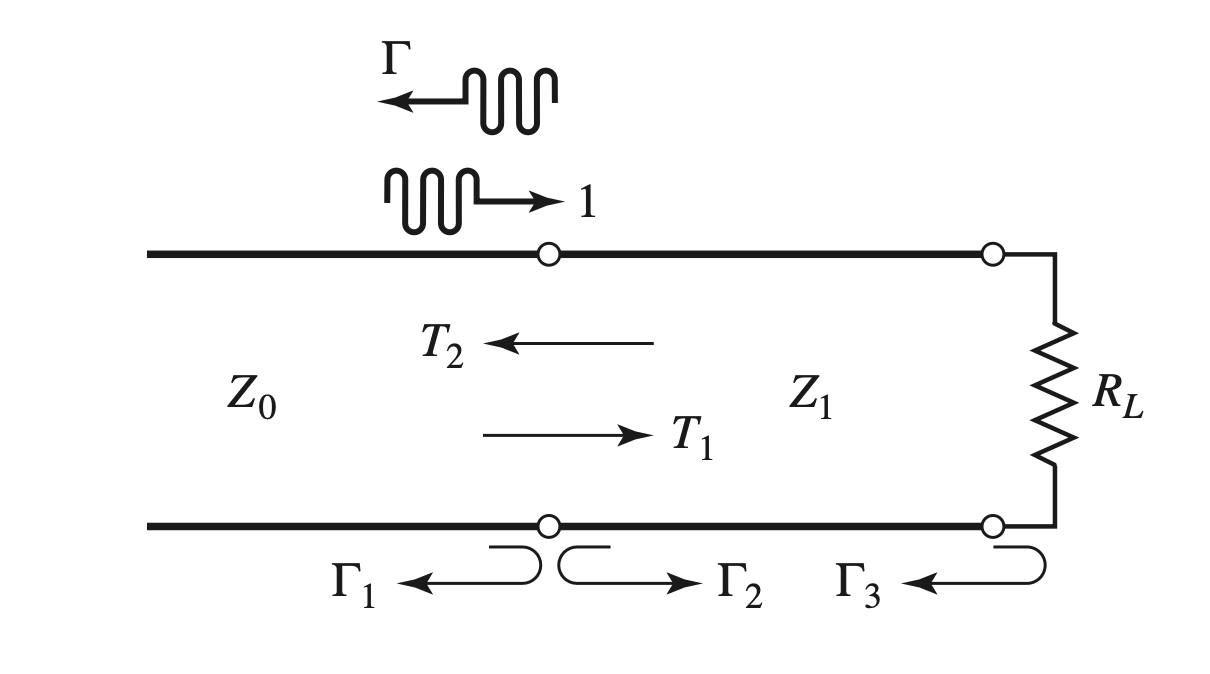
Partial Coefficients
$$ \begin{gather} \begin{aligned} \Gamma_1 &= \frac{ Z_1 - Z_0 }{ Z_1 + Z_0 } \\ \Gamma_2 &= - \Gamma_1 \\ \Gamma_3 &= \frac{ R_L - Z_1 }{ R_L + Z_1 } \end{aligned} \end{gather} $$
$$ \begin{gather} \begin{aligned} T_1 &= \frac{ 2Z_1 }{ Z_1 + Z_0 } \\ T_2 &= \frac{ 2Z_0 }{ Z_1 + Z_0 } \end{aligned} \end{gather} $$
Total Reflection Coefficients
$$ \begin{gather} \begin{aligned} \Gamma &= \Gamma_1 - T_1 T_2 \Gamma_3 + T_1 T_2 \Gamma_2 \Gamma_3^2 \\ &= \Gamma_1 - T_1 T_2 \Gamma_3 \sum_{ n=0 }^{ \infin } (- \Gamma_2 \Gamma_3 )^n \\ &= \Gamma_1 - \frac{ T_1 T_2 \Gamma_3 }{ 1 + \Gamma_2 \Gamma_3 } \\ &= \frac{ \Gamma_1 + \Gamma_1 \Gamma_2 \Gamma_3 - T_1 T_2 \Gamma_3 }{1 + \Gamma_2 \Gamma_3 } \\ \end{aligned} \end{gather} $$
- 其中,分子可以写成
$$ \begin{gather} \begin{aligned} \Gamma_1 - \Gamma_3( \Gamma_1^2 + T_1T_2) &= \frac{ 2(Z_1^2 - Z_0 R_L) }{ (Z_1 + Z_0)(R_L + Z_1) } \end{aligned} \end{gather} $$
- 可以看出,当$Z_1 = \sqrt{ Z_0 R_L }$时,Impedance Match
Generator and Impedance Mismatches
Power Expression
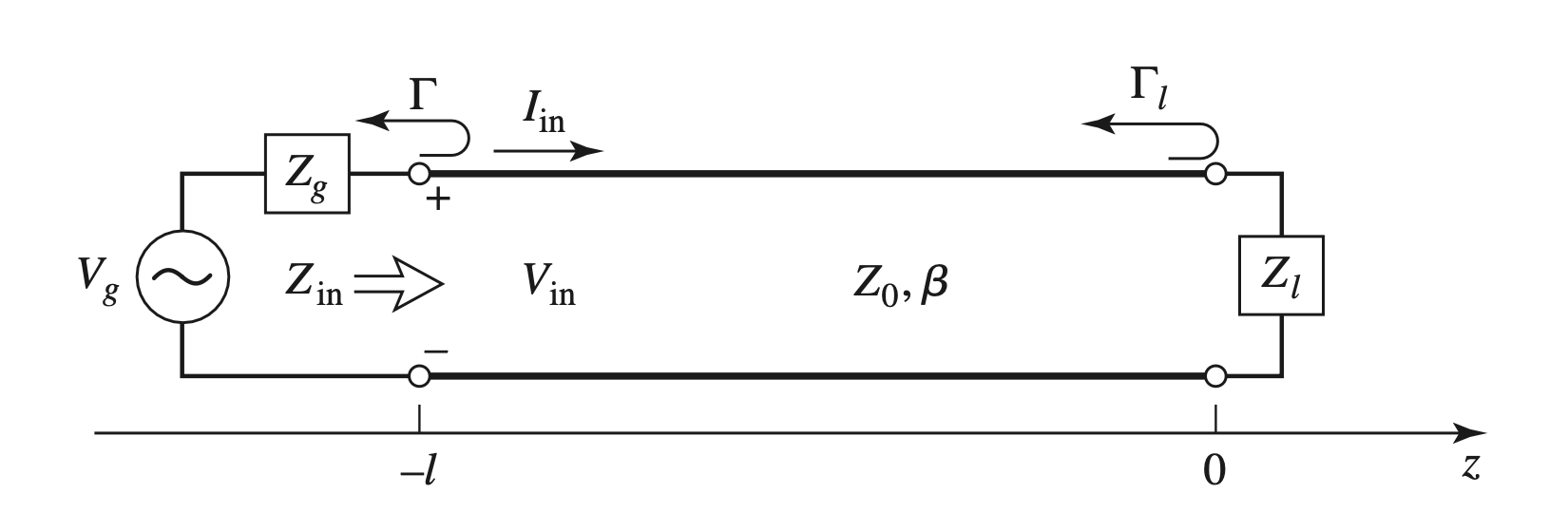
Input Voltage
$$ \begin{gather} \begin{aligned} Z_{in} &= Z_0 \frac{ 1 + \Gamma_l e^{-2j \beta l} }{ 1 - \Gamma_l e^{-2j \beta l} } \\ V_{in} &= V(-l) \\ &= V_0^+( e^{j \beta l} + \Gamma_l e^{-j \beta l}) \\ &= \frac{ Z_{in} }{ Z_{in} + Z_g } V_g \\ \therefore V_0^+ &= V_g \frac{ Z_0 }{ Z_0 + Z_g } \frac{ e^{-j \beta l} }{ 1 + \Gamma_l \Gamma_g e^{-2j \beta l} } \\ \Gamma_l &= \frac{ Z_l - Z_0 }{ Z_l + Z_0 }, \Gamma_g = \frac{ Z_g - Z_0 }{ Z_g + Z_0 } \end{aligned} \end{gather} $$
Power Expression
$$ \begin{gather} \begin{aligned} P &= \frac{ 1 }{ 2 } \mathcal{Re} \Big\lbrace V_{in} I_{in}^* \Big\rbrace \\ &= \frac{ 1 }{ 2 } V_{in}^2 \mathcal{Re} \Big\lbrace \frac{ 1 }{ Z_{in} } \Big\rbrace \\ &= \frac{ 1 }{ 2 } | V_g|^2 \frac{ |Z_0|^2 }{ |Z_0 + Z_g|^2 } \mathcal{Re} \Big\lbrace \frac{ 1 }{ Z_{in} } \Big\rbrace \\ &= \frac{ 1 }{ 2 } |V_g|^2 \frac{ R_{in} }{ (R_{in} + R_g)^2 + (X_{in} + X_g)^2} \end{aligned} \end{gather} $$
Impedance Match
- $Z_l = Z_0$
- $Z_{in} = Z_0$
$$ \begin{gather} \begin{aligned} P &= \frac{ 1 }{ 2 } |V_g|^2 \frac{ Z_0 }{ (Z_0 + R_g)^2 + X_g^2 } \end{aligned} \end{gather} $$
- $Z_g = Z_{in}$
$$ \begin{gather} \begin{aligned} P &= \frac{ 1 }{ 2 } |V_g|^2 \frac{ R_g }{ 4(R_g + X_g)^2 } \end{aligned} \end{gather} $$
- Conjugate Matching
$$ \begin{gather} \begin{aligned} \frac{ \partial P }{ \partial R_{in} } &=0 \Longrightarrow R_g^2 - R_{in}^2 = -(X_{in} + X_g)^2 \\ \frac{ \partial P }{ \partial X_{in} } &= 0 \Longrightarrow X_{in} (X_{in} + X_g) = 0 \\ \therefore Z_{in} &= Z_g^* \\ P_{min} &= \frac{ |V_g|^2 }{ 8 R_g } \end{aligned} \end{gather} $$
Lossy Transmission Lines
Low-Loss Line
$$ \begin{gather} \begin{aligned} \gamma &= \alpha + j \beta \\ &= \sqrt{ (R + j \omega L) ( G + j \omega C) } \\ &= j \omega \sqrt{ LC } \sqrt{ 1 - \frac{ RG}{ \omega^2 L C } - j ( \frac{ R }{ \omega L } + \frac{ G }{ \omega C })} \\ &\approx j \omega \sqrt{ LC } \sqrt{ 1 - j ( \frac{ R }{ \omega L } + \frac{ G }{ \omega C }) } \\ &\approx j \omega \sqrt{ LC } \Big[ 1 - \frac{ j }{ 2 } ( \frac{ R }{ \omega L } + \frac{ G }{ \omega C }) \Big] \end{aligned} \end{gather} $$
$$ \begin{gather} \begin{aligned} \alpha &= \frac{ 1 }{ 2 } ( \frac{ R }{ \omega L } + \frac{ G }{ \omega C }) \\ \beta &= \omega \sqrt{ LC } = k \end{aligned} \end{gather} $$
Distortionless Line
- $\dfrac{ R }{ L } = \dfrac{ G }{ C }$
$$ \begin{gather} \begin{aligned} \gamma &\approx j \omega \sqrt{ LC } \sqrt{ 1 - j \frac{ R }{ \omega L } } \\ \alpha + j\beta &= R \sqrt{ \frac{ C }{ L } } + j \omega \sqrt{ L C } \end{aligned} \end{gather} $$
Terminated Lossy Line
- Reflection Coefficient
- 假设Loss很小, $\beta \approx 0, \gamma \approx \alpha$
$$ \begin{gather} \begin{aligned} \Gamma(l) &= | \Gamma| e^{-2 \gamma l} \end{aligned} \end{gather} $$
- Power
$$ \begin{gather} \begin{aligned} P_{in} &= \frac{ 1 }{ 2 } \mathcal{Re} \Big\lbrace V(-l) I’(-l) \Big\rbrace \\ &= \frac{ |V_0^+|^2 }{ 2 Z_0 } (e^{2 \alpha l} - | \Gamma|^2 e^{-2 \alpha l}) \\ &= \frac{ |V_o^+|^2 }{ 2 Z_o }(1 - | \Gamma(l)|^2)e^{-2 \alpha l} \\ P_L &= \frac{ 1 }{ 2 } \mathcal{Re} \Big\lbrace V(0) I’(0) \Big\rbrace \\ &= \frac{ |V_o^+|^2 }{ 2 Z_0 } (1 - |\Gamma|^2) \\ P_{loss} &= P_{in} - P_L \\ &= \frac{ |V_0|^2 }{ 2Z_0 } \Big[ (e^{2 \alpha l} - 1) + | \Gamma|^2 ( 1- e^{-2 \alpha l}) \Big] \end{aligned} \end{gather} $$
- 第一项是Incident Power Loss, 第二项是Reflected Power Loss
Perturbation Methods for Calculating Attenuation
| Category | Concept |
|---|---|
| $P(z)$ | Power Flow on the Transmission Line |
| $P_l(z)$ | Power Loss per unit length |
$$ \begin{gather} \begin{aligned} P(z) &= P_0 e^{-2 \alpha z} \\ P_l(z) &= - \frac{ \partial P }{ \partial z } \\ &= 2 \alpha P(z) \\ \therefore \alpha &= \frac{ P_l }{ 2 P(z) } \\ &= \frac{ P_l(0) }{ 2 P(0) } \\ &= \frac{ P_l(z = 0) }{ 2 P_o } \end{aligned} \end{gather} $$
Transients on Transmission Line
Reflection of Pulses From a Terminated Transmission Line
- $Z_S = Z_L = Z_0$
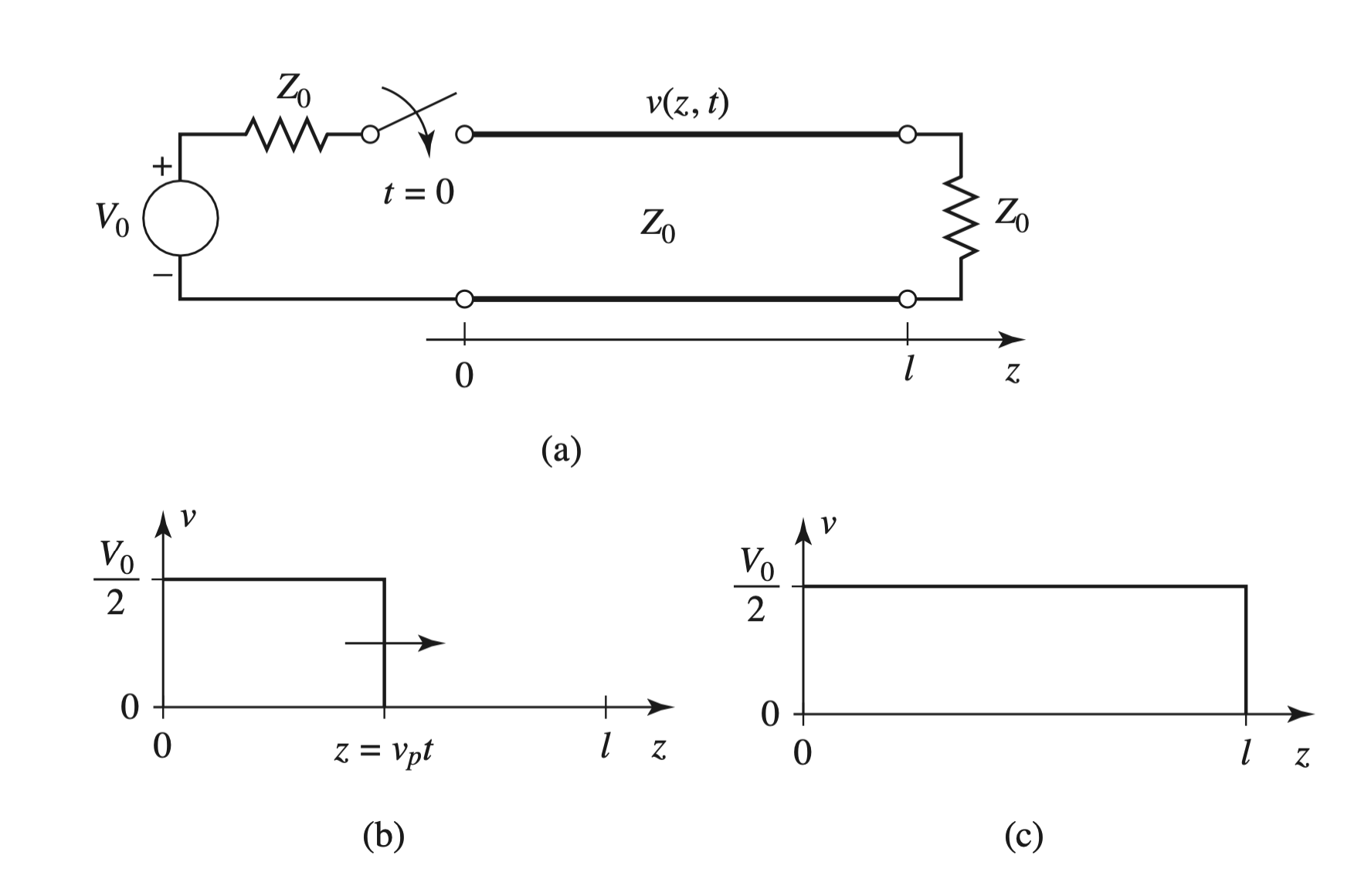
- Short-Circuit, $\Gamma = -1$
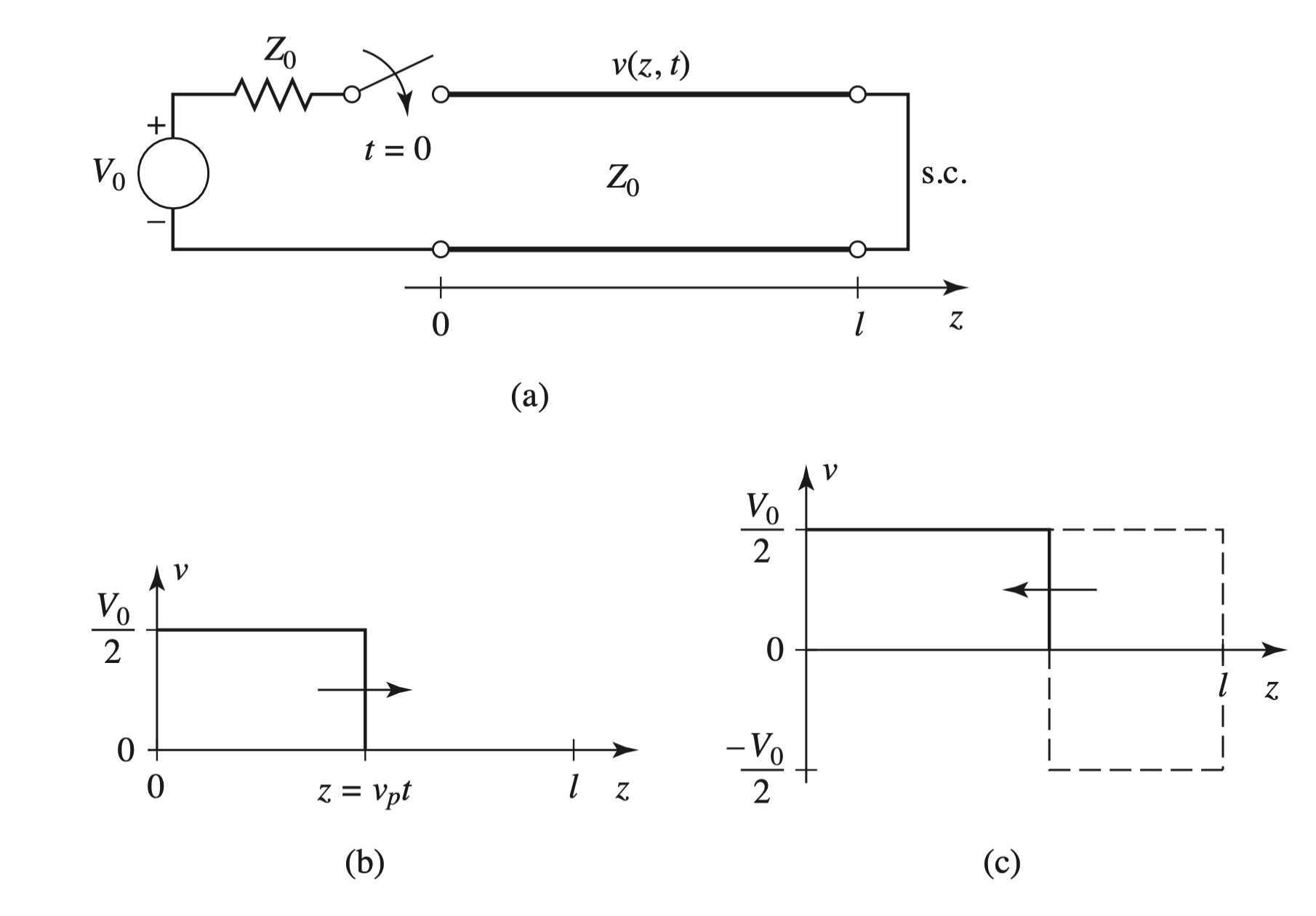
- Open-Circuit, $\Gamma = 1$
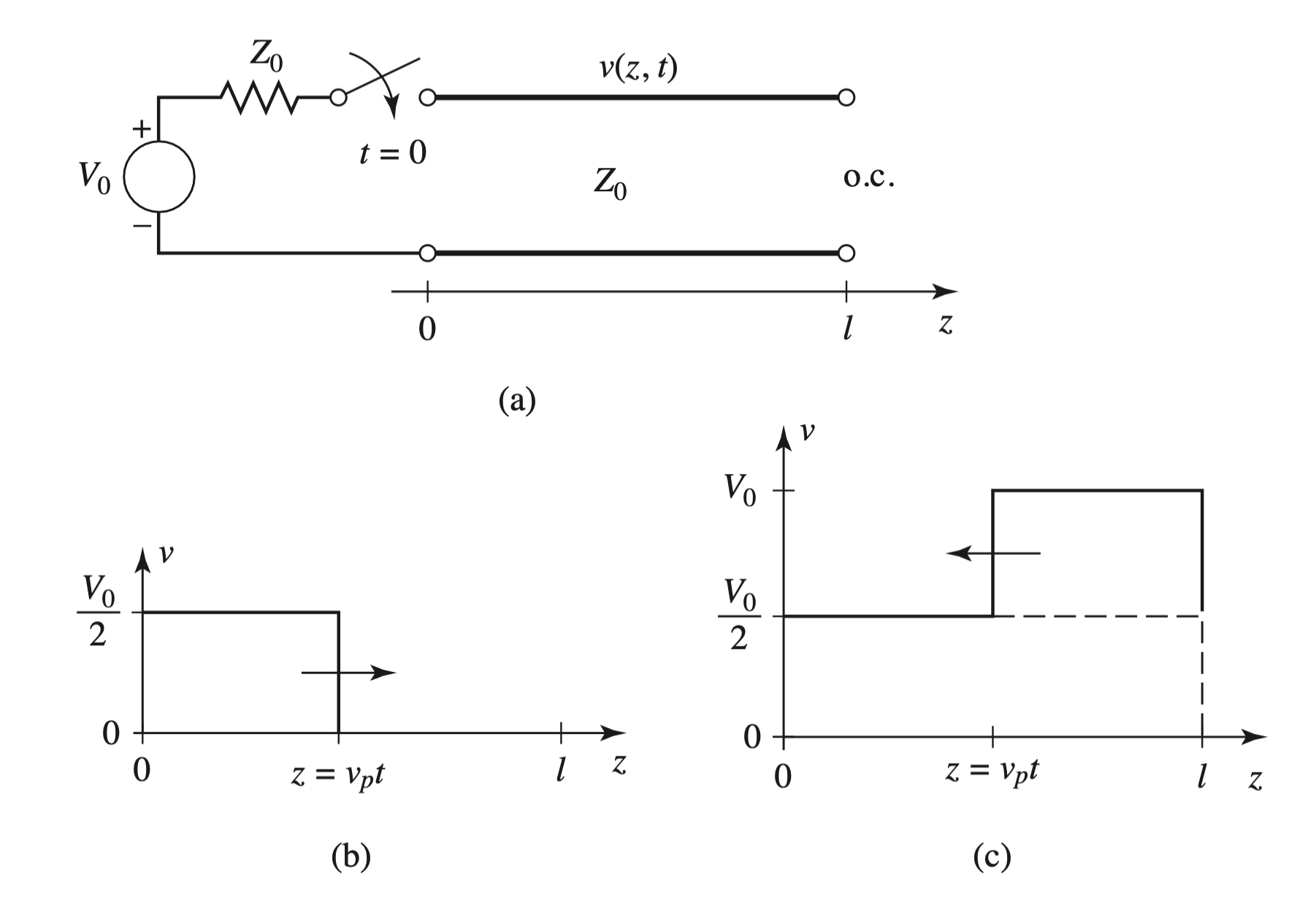
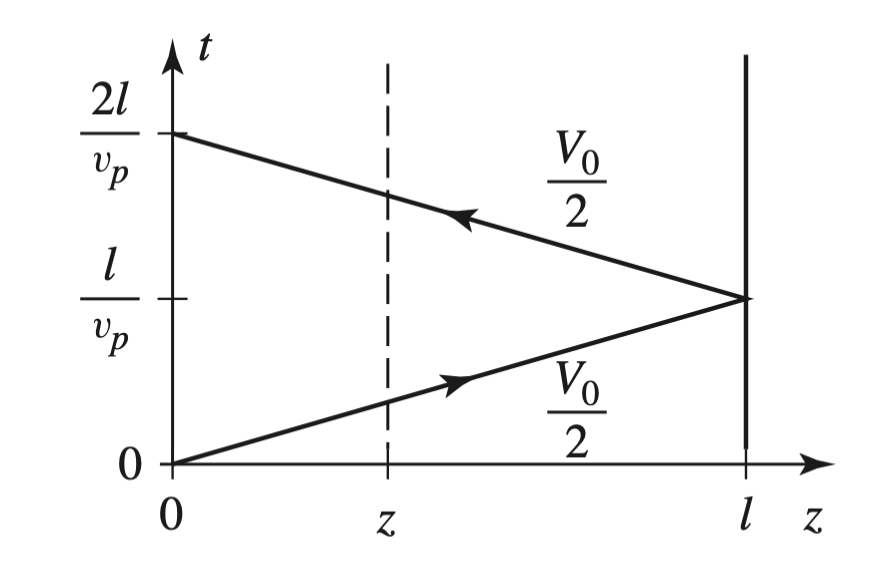
Bounce Diagrams for Transient Circuits
- Bounce Diagram for Open-Circuit
Appendix
部分微分方程解法

Triogonometric Function Formulas
$$ \begin{gather} \begin{aligned} tanh(x) &= \frac{ e^x - e^{-x} }{ e^x + e^{-x}} \\ atans2(x) &= \begin{cases} tan^{-1}( \dfrac{ y }{ x }) & x > 0 \\ tan^{-1}( \dfrac{ y }{ x }) + \pi & x < 0, y \ge 0 \\ tan^{-1}( \dfrac{ y }{ x }) - \pi & x < 0, y < 0 \\ Error & x = 0, y =0 \end{cases} \end{aligned} \end{gather} $$