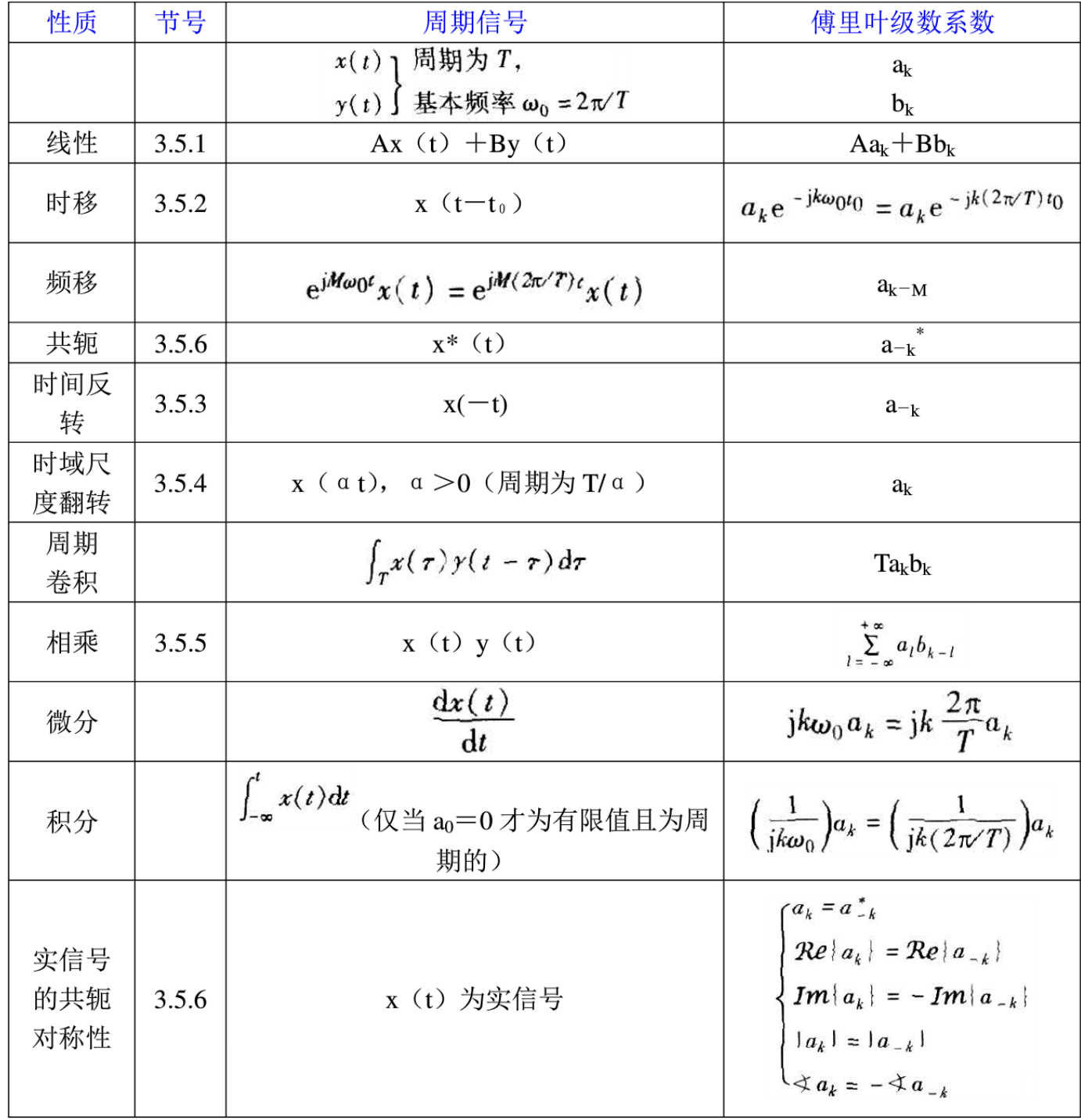
LTI 对于复指数信号的响应
响应
$$ \begin{gather} \begin{aligned} e^{st} &\longrightarrow H(s) e^{st} \\ z^n &\longrightarrow H(z) z^n \end{aligned} \end{gather} $$
-
复指数函数是LTI系统的特征函数
-
当系统输入为 $e^{st}$时,响应应具有$Ae^{st}$的形式
Transfer Function $H(z) / H(s)$
Computation
- 当输入$x(t) = e^{st}, x[n] = z^n$时
$$ \begin{gather} \begin{aligned} H(s) &= H(j \omega)\int_{ - \infin }^{ \infin } h(\tau) e^{-s \tau} d\tau \\ H(z) &= H(e^{j \omega})\sum_{ k = - \infin }^{ \infin } h[k] z^{-k} \end{aligned} \end{gather} $$
- 当$s$和$z$为一般复数时,$H$为系统函数
Transfer Function and FS (叠加性质)
$$ \begin{gather} \begin{aligned} y(t) &= [\sum_{ k = - \infin }^{ \infin } a_k H( jk \omega_0)] x(t) \\ y[n] &= [\sum_{ k = - \infin }^{ \infin } a_k H( jk \omega_0)] x[n] \end{aligned} \end{gather} $$
连续时间周期信号的傅立叶级数表示
成谱波关系的复指数信号的线性组合
一般周期信号的傅立叶级数表示
$$ \begin{equation} x(t) = \sum_{k = -\infin}^{ \infin} a_ke^{j k \omega 0 t} = \sum{k = -\infin}^{ \infin} a_ke^{j k \dfrac{2\pi}{T} t} \end{equation} $$
- $k = \pm N$这两项叫做N次谐波分量
实信号的傅立叶级数表示
- 实信号的傅立叶级数满足$a_k = a_{-k}^*$
$$ \begin{aligned} x(t) &= a_0 + \sum_{k=1}^{ \infin} \Big[ a_k e^{j k \omega _0 t} + a_k e^{-jk \omega 0 t} \Big] \\ &= a_0 + 2 \sum{k=1}^{ \infin} \mathbb R \lbrace a_ke^{j k \omega_0 t} \rbrace \end{aligned} $$
- 现在,让, $a_k = A_k e^{j\theta_k}$
$$ \begin{equation} x(t) = a_0 + 2 \sum_{k = 1}^{ \infin} A_k cos(k \omega _0 t + \theta_k) \end{equation} $$
- 让$a_k = B_k + jC_k$
$$ \begin{equation} x(t) = a_0 + 2 \sum_{k=1}^{ \infin} \Big[ B_k cos ( k\omega_0 t ) -j C_k sin(k \omega_0 t) \Big] \end{equation} $$
连续时间周期信号傅里叶级数表示的确定
$$ \begin{equation} a_k = \frac{1}{T} \int_{T} e^{-jk \omega 0 t} x(t) dt = \frac{1}{T} \int{T} e^{-jk \dfrac{2\pi}{T} t} x(t) dt \end{equation} $$
- 其中, $a_0 = \dfrac{1}{T} \int_{T} x(t) dt$, 表示为直流分量
FS Convergence - Diriheli Condition
- 函数必须在任意时间内绝对可积, 即
$$ \begin{equation} \int_T |x(t)| < \infin \end{equation} $$
-
在任意时间内,函数的最大值和最小值必须是有限的
-
在任意时间内,函数必须有有限个不连续点, 且这些点的值必须是有限值
连续时间周期信号傅立叶级数性质
Paswal’s Theorem
- 周期信号的平均功率 = 各个谐波信号的平均功率之和
$$ \begin{equation} \underset{ T \longrightarrow \infin }{lim}\frac{ 1 }{ T }\int_{ T }^{ } |x(t)|^2 dt = \int_{ T }^{ } |a_k|^2 dt \end{equation} $$
变换性质
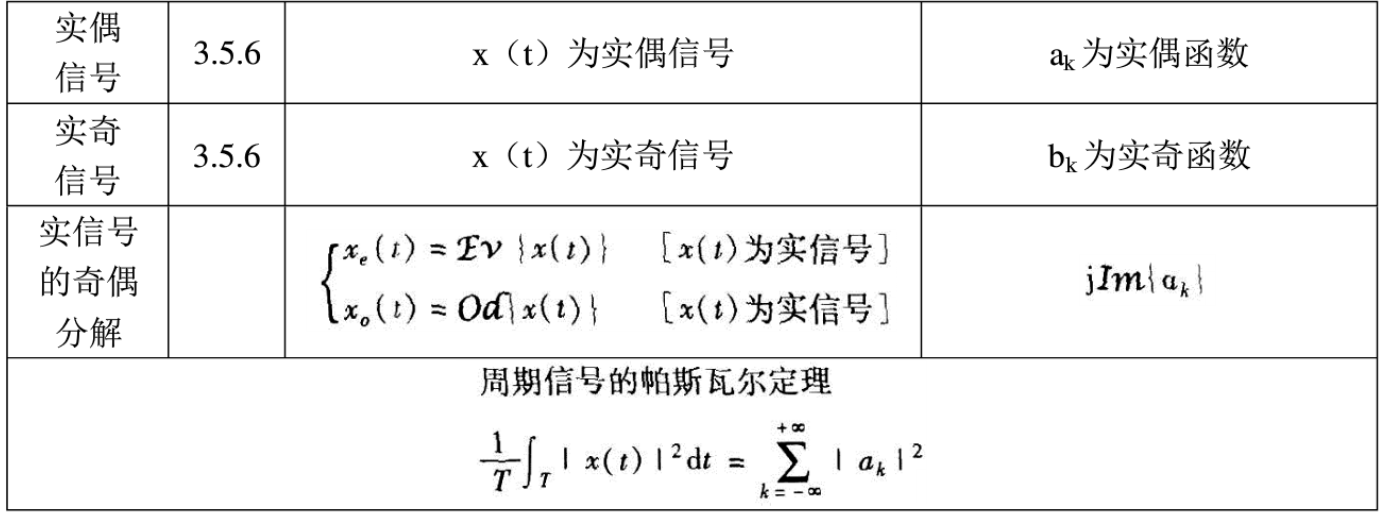
| $x(t)$ | $a_k$ |
|---|---|
| 实偶函数 | 实偶函数 |
| 实奇函数 | 纯虚奇函数 |
FS of Some Important Functions
Square Wave
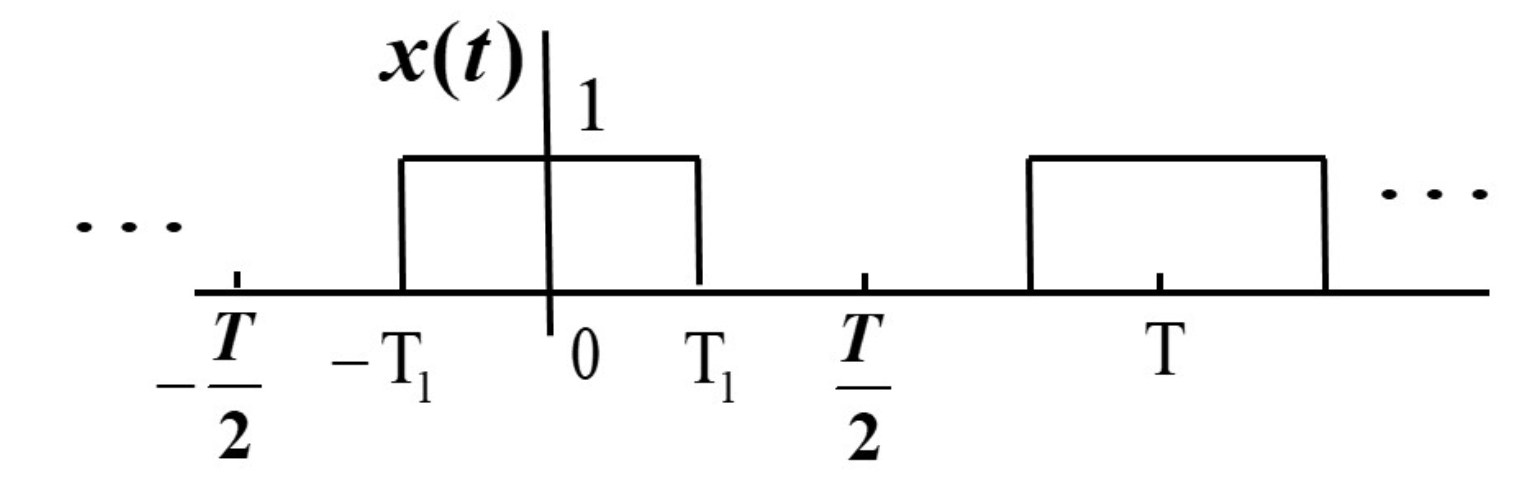
$$ \begin{equation} a_k = \frac{ sin( k \omega_0 T_1) }{ k \pi } \end{equation} $$
Impulse Train
$$ \begin{equation} x(t) = \sum_{ k = - \infin }^{ \infin } \delta (t-kT) \overset{ FS }{ \longleftrightarrow } a_k = \frac{ 1 }{T } \end{equation} $$
Others
Constant Function
$$ \begin{equation} x(t) = C \overset{ FS }{ \longleftrightarrow } a_k = \begin{cases} 0 & k \neq 0 \\ C & k = 0 \end{cases} \end{equation} $$
离散时间信号的傅立叶级数表示
谐波信号
$$ \begin{equation} \begin{aligned} x[n] &= \sum_{ k=(N) }^{ }a_k e^{jk \omega_0 n} = \sum_{ k=(N) }^{ }a_k e^{jk \dfrac{ 2\pi }{ N } n} \end{aligned} \end{equation} $$
周期信号
$$ \begin{align} x[n] &= \sum_{ k=(N) }^{ }a_k e^{jk \omega_0 n} = \sum_{ k=(N) }^{ }a_k e^{jk \dfrac{ 2\pi }{ N } n} \\ a_k &= \frac{ 1 }{ N} \sum_{ k = (N) }^{ } x[n] e^{-j k \omega_0 n} \end{align} $$
性质

Filter
Transfer Function Decomposition
- For a Cascode System
$$ \begin{equation} H(j \omega) = H_1(j \omega) H_2(j \omega) H_3 (j \omega) = |H_1(j \omega) H_2(j \omega) H_3 (j \omega)| \cdot e^{j ( \angle H_1(j \omega) + \angle H_2 (j \omega) + H_3 (j \omega))} \end{equation} $$