Representation of Aperiodic Signals
傅立叶级数求解
- 假设$\widehat {x}{ ~ } (t)$ 代表$x(t)$ 在一个周期内的函数
$$ \begin{aligned} \widehat { a_k }{~} &= \frac{ 1 }{ T } \int_{ - T/2 }^{ T / 2} x(t) e^{-jk \omega t} dt \end{aligned} $$
- 当$T \longrightarrow \infin$,信号其实就是非周期信号
$$ \begin{aligned} a_k &= \widehat { a_k }{~} = \frac{ 1 }{ T } \int_{- \infin }^{ \infin } x(t) e^{-jk \omega t}dt \end{aligned} $$
Fourier Transform of Aperiodic Signals
FT
$$ \begin{gather} \begin{aligned} x(t) \overset{ F }{ \longleftrightarrow }X(j \omega) &= T a_k = \int_{ - \infin }^{ \infin } x(t) e^{-j \omega t} dt \\ &= \sum_{ n = - \infin }^{ \infin } x[n] e^{-j \omega n} \\ &= |H(j \omega)| e^{ j\angle H(j \omega)} \end{aligned} \end{gather} $$
FT of Aperiodic Signals
$$ \begin{aligned} a_k &= \frac{ 1 }{ T } X(j k \omega_0) \\ \therefore \widehat { x(t) }{ ~ } &= \sum_{ k }^{ } a_k e^{jk \omega t} \\ &= \frac{ 1 }{ 2\pi } \sum_{ k = - \infin }^{ \infin } X(j \omega_0 t) e^{jk \omega_0 t} \omega_0 \end{aligned} $$
$$ \begin{gather} \begin{aligned} x(t) &= \frac{ 1 }{ 2 \pi } \int_{ - \infin }^{ \infin } X(j \omega) e^{j \omega t} d \omega \\ x[n] &= \frac{ 1 }{ 2\pi } \int_{ - \infin }^{ \infin } X(j \omega) e^{j \omega n} d \omega \end{aligned} \end{gather} $$
存在FT的条件 - Dirichlet Conditions
- C-T
- 反例: $x(t) = e^t u(t)$ 没有FT
- D-T
- 以下条件满足其一即可
$$ \begin{gather} \begin{aligned} \int_{ - \infin }^{ \infin } |x(t)| dt \le \infin \\ \int_{ - \infin }^{ \infin } |x(t)|^2 dt \le \infin \end{aligned} \end{gather} $$
Properties of FT
- C-T
- If $x(t)$ is Real
$$ \begin{gather} \begin{aligned} x(t) &= x_e(t) + x_o(t) \\ X(j \omega) &= X_R(j \omega) + j X_I ( j \omega) \\ x_e(t) &\overset{ F }{ \longleftrightarrow } X_R(j \omega) = X_e(j \omega) \\ x_o(t) &\overset{ F }{ \longleftrightarrow } X_I(j \omega) = X_o(j \omega) \end{aligned} \end{gather} $$
- FT的反向求法
$$ \begin{aligned} f(t) = 1 &\overset{ F }{ \longleftrightarrow } X(j \omega) = 2 \pi \delta (\omega) \\ FT^{-1} [ 2 \pi \delta ( \omega)] &= \frac{ 1 }{ 2 \pi }\int_{ - \infin }^{ \infin } X(j \omega) e^{j \omega t} d \omega = 1 \end{aligned} $$
$$ \begin{gather} \begin{aligned} \delta ( \omega) &= \frac{ 1 }{ 2 \pi } \int_{ - \infin }^{ \infin } e^{-j \omega t} d \omega \end{aligned} \end{gather} $$
- 其他性质
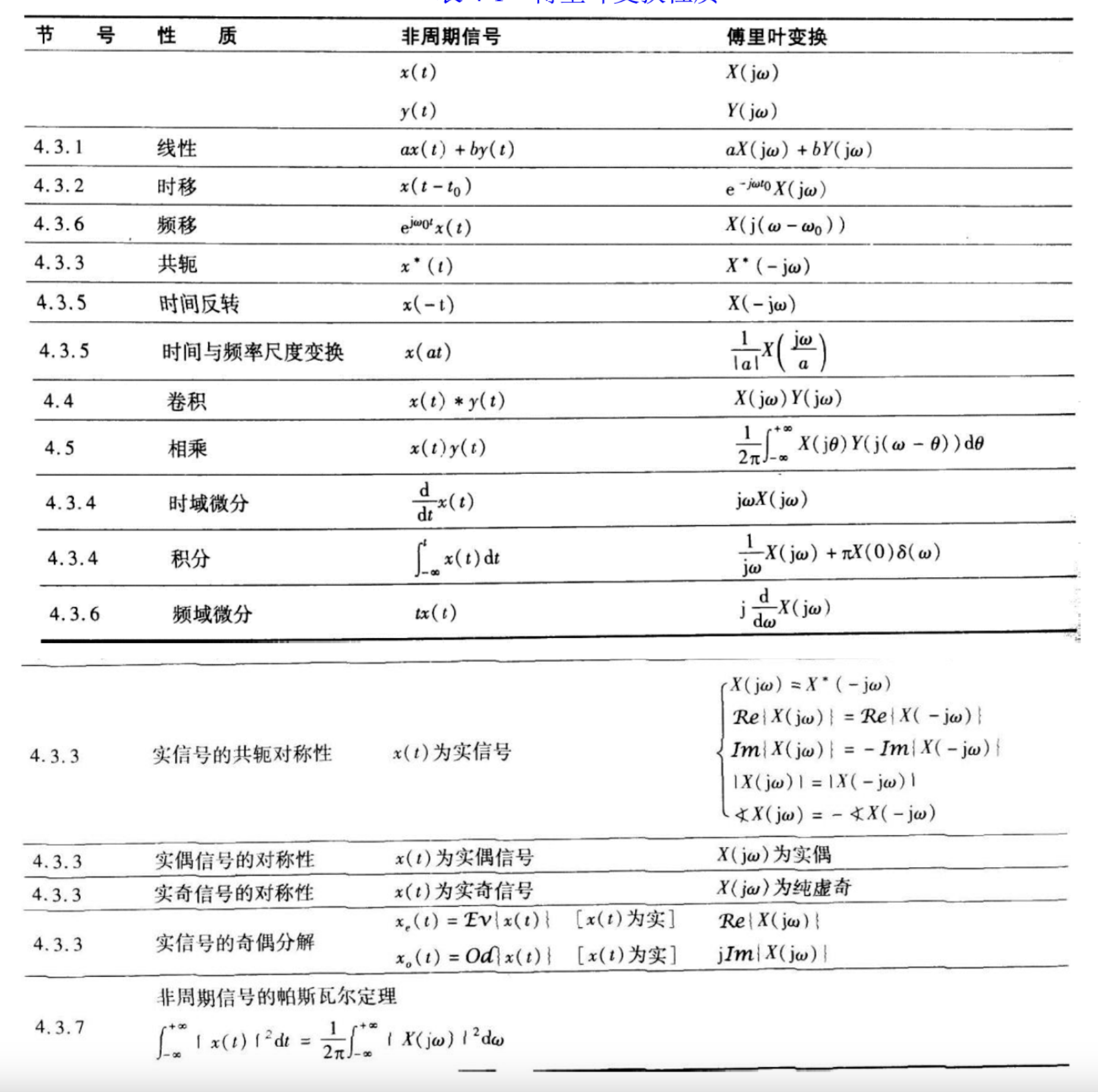
- D-T
- Periodicity
$$ \begin{equation} X[e^{j (\omega + 2 \pi)}] = X(e^{j \omega}) \end{equation} $$
- Duality
$X(e^{j \omega}) \longleftrightarrow x[n]$
Sinc & Sa Functions
$$ \begin{gathered} \begin{align} sinc( \theta) &= \frac{ sin(\pi \theta) }{ \theta} \overset{ F }{ \longleftrightarrow } X(j \omega) = 2T_1 sinc( \frac{ \omega T_1 }{ \pi }) \\ sa( \phi) &= \frac{ sin( \phi) }{ \phi} \overset{ F }{ \longleftrightarrow } X(j \omega) = 2 T_1 sa( \omega T_1) \end{align} \end{gathered} $$
FT of Periodic Signals
Definition
- 假设$X(j \omega) = 2 \pi \delta ( \omega - \omega_0)$
$$ \begin{aligned} x(t) &= \frac{ 1 }{ 2 \pi }\int_{ - \infin }^{ \infin } X(j \omega) e^{j \omega t} \\ &= e^{ j \omega_0 t} \end{aligned} $$
- 再假设 $X(j \omega) = \sum_{ k = -\infin }^{ \infin } 2 \pi a_k \delta ( \omega - k \omega_0)$
$$ \begin{aligned} x(t) &= \int_{ - \infin }^{ \infin } a_k e^{j k \omega t} \end{aligned} $$
- 因此,周期信号的傅立叶转换为
$$ \begin{gather} \begin{aligned} X(j \omega) &= \sum_{ k = - \infin }^{ \infin } 2 \pi a_k \delta ( \omega - k \omega_0) \\ X(e^{j \omega}) &= \sum_{ k= - \infin }^{ \infin } 2 \pi a_k \delta ( \omega - k \frac{ 2 \pi }{ N }) \end{aligned} \end{gather} $$
Fundamental FT & FS

System Characterized by LCCDE
Frequency Response
$$ \begin{aligned} \sum_{ k = 0 }^{ K} a_k \frac{ d^ky}{ dt^k} &= \sum_{ k = 0}^{ M} b_k \frac{ d^kx}{ dt^k} \\ \sum_{ k = 0 }^{K} a_k \cdot F \lbrace \frac{ d^k y }{ dt^k} \rbrace &= \sum_{ k =0 }^{ M} b_k \cdot F \lbrace \frac{ d^k x }{ dt^k } \rbrace \\ Y(j \omega) \sum_{ k = 0 }^{K} a_k (j \omega)^k &=X(j \omega) \sum_{ k = 0 }^{ M} b_k (j \omega)^k \end{aligned} $$
$$ \begin{equation} H(j \omega) = \frac{ Y(j \omega) }{ X(j \omega) } = \frac{ \sum_{ k = 0 }^{ M}b_k ( j \omega)^k }{\sum_{ k = 0 }^{ K }a_k ( j \omega)^k} \end{equation} $$
Time/Frequency Domain Characteristic
Magnitude, Phase, Logarithm, Bode Plots
$$ \begin{gather} \begin{aligned} Y(j \omega) &= |X(j \omega) H(j \omega)| \\ \angle Y(j \omega) &= \angle X(j \omega) + \angle H(j \omega) \\ lg|Y(j \omega)| &= lg|H(j \omega)| + lg|X(j \omega)| \end{aligned} \end{gather} $$
-
通常,Phase包含更多的信息
-
Bode Plots: $20 lg \Big[ H(j \omega)| \Big] - \omega$
Phase Shifting & Group Delay
| 名称 | 概念 |
|---|---|
| Linear Phase | $\angle H(j \omega) = k \omega$ |
| Non-Linear Phase | $\angle H(j \omega) \approx- \phi - \omega \alpha$ |
$$ \begin{gather} \begin{aligned} \angle H(j \omega) &= \omega \cdot t \\ \tau( \omega) &= - \frac{ d \Big\lbrace \angle H(j \omega) \Big\rbrace}{ d \omega } \end{aligned} \end{gather} $$
Filters
LPF
Introduction
$$ \begin{gather} \begin{aligned} H(j \omega) &= \begin{cases} 1 & \omega < | \omega_0 | \\ 0 & \omega > | \omega_0 | \end{cases} \\ h(t) &= \frac{ sin( \omega_c t) }{ \pi t} \end{aligned} \end{gather} $$
- $Casulaity \longleftrightarrow Real-Time$
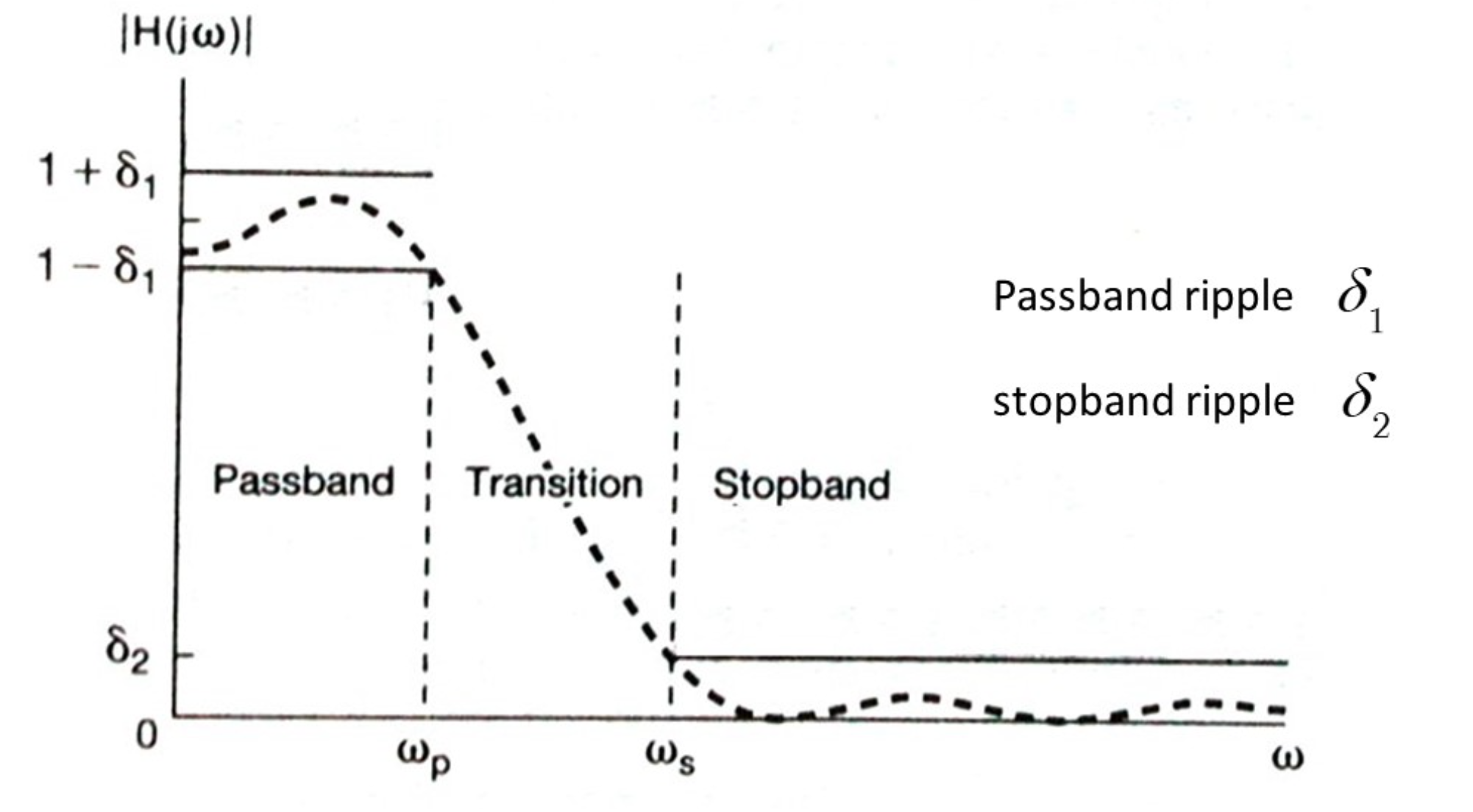
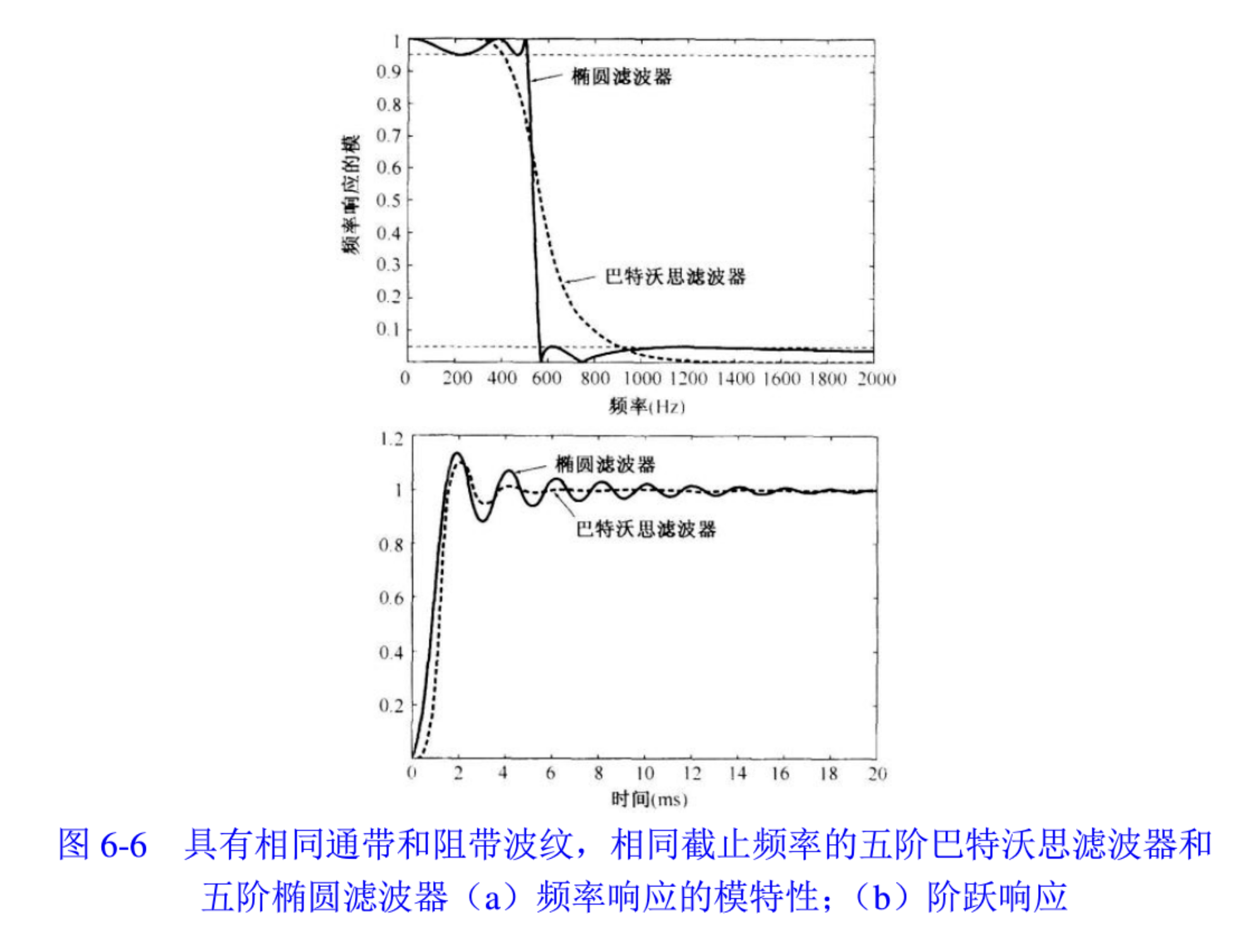
Butterworth & Elliptic LPW
Appendix
Partial-Fraction Expansions
Case I
$$ \begin{gather} \begin{aligned} Y(j \omega) &= \frac{ A }{ a + j \omega } + \frac{ B }{b + j \omega} \\ &= \frac{ C }{ (a+ j \omega) ( b + j \omega)} \end{aligned} \end{gather} $$
Case II
$$ \begin{gather} \begin{aligned} G(v) &= \frac{ A_1 }{ v -p_1 }+ \frac{ A_2 }{v -p_2} + \frac{ A_3 }{ v - p_3 } = \frac{ b_2 v^2 + b_1v + b_0 }{ (v-p_1)(v-p_2)(v-p_3) } \\ A_1 &= \frac{ b^2 v + b_1 v + b_0 }{ (p_1 - p_2)(p_1 - p_3) } \end{aligned} \end{gather} $$
Case III
$$ \begin{gather} \begin{aligned} G(v) &= \frac{ A_1 }{ v - p_1 } + \frac{ A_2 }{ (v - p_1)^2} + \frac{ A_3 }{ v - p_2} = \frac{ b_2 v^2 + b_1 v + b_0}{ (v-p_1)^2(v-p_2) }\\ A_1 &= \frac{ d }{ dv } \Big\lbrace G(v) \cdot (v-p_1)^2 \Big\rbrace , v = p_1\\ A_2 &= G(v) \cdot (v-p_1)^2 , v = p_1\\ A_3 &= G(v) \cdot (v-p_2), v = p_2 \end{aligned} \end{gather} $$
Plural Modulus
$$ \begin{gather} \begin{aligned} |\frac{ A }{ B + jC }| &= \frac{ |A| }{ \sqrt{ B^2 + C^2} } \\ |\frac{ 1 }{ 1 + a \cdot e^{j \omega} }| &= \frac{ 1 }{ 1 + a } \end{aligned} \end{gather} $$