Impedance & Admittance Matrix
Expressions & Explanations
$$ \begin{gather} \begin{aligned} [V] &= [Z][I] \\ [I] &= [Y][V] \\ [Z] &= [Y]^{-1} \\ Z_{ij} &= \frac{ V_i }{ I_j } , I_k = 0, k \neq j \\ Y_{ij} &= \frac{ I_i }{ V_j }, V_k = 0, k \neq j \end{aligned} \end{gather} $$
| Category | Concept |
|---|---|
| $Z_{ij}$ | 用$I_j$驱动Port j, 开路其他所有端口,测量$V_i$; 表示其他端口均开路时的$i$到$j$的Transfer Impedance |
| $Z_{ii}$ | 开路其他所有端口时Port $i$的阻抗 |
| $Y_{ij}$ | 用$V_j$驱动Port j, 短路其他所有端口,测量$I_i$; 表示其他端口均短路时的$i$到$j$的Transfer Admittance |
Reciprocal & Lossless Network
$$ \begin{gather} \begin{aligned} Reciprocal \Longrightarrow [Y] = [Y]^t \\ Lossless \Longrightarrow \mathcal{Re} \Big\lbrace P_{avg} \Big\rbrace &= 0 \\ P_{avg} &= \frac{ 1 }{ 2 } [V]^t [I]^* \\ &= \frac{ 1 }{ 2 } [I]^t [Z]^t[I]^* \\ &= \frac{ 1 }{ 2 } \sum_{ n = 1 }^{ N } \sum_{ m = 1 }^{ N } I_m Z_{mn} I_n^* \\ \mathcal{Re} \Big\lbrace P_{avg} \Big\rbrace &= \frac{ 1 }{ 2 } |I_n|^2 \mathcal{Re} \Big\lbrace Z_{mn} \Big\rbrace \\ &= 0 \\ \therefore \mathcal{Re} \Big\lbrace Z_{mn} \Big\rbrace &= 0 \end{aligned} \end{gather} $$
Scattering Matrix
Expressions & Explanations
Definition
$$ \begin{gather} \begin{aligned} [V^-] &= [S] [V^+] \\ S_{ij} &= \frac{ V^-_i }{ V^+_j} , V_k^+ = 0, k \neq j \end{aligned} \end{gather} $$
S - Z Conversion
- 假设所有端口的Characteristic Impedance $Z_{0n} = 1$
$$ \begin{gather} \begin{aligned} [Z][I] &= [Z][V^+] - [Z][V^-] \\ [V] &= [V^+] + [V^-] \\ \therefore [S] &= ([Z] + [U])^{-1} ( [Z] - [U]) \\ [Z] &= ([U]+ [S])([U] - [S])^{-1} \end{aligned} \end{gather} $$
Reciprocal & Lossless Network
- 经过证明可以得到, Scattering Matrix 是一个Reciprocal Network
$$ \begin{gather} \begin{aligned} [S] &= [S]^t \end{aligned} \end{gather} $$
- 若Scattering Matrix是一个Lossless Network, 则其必然是Unitary Matrix
$$ \begin{gather} \begin{aligned} [S]^* &= \Big\lbrace [S]^t \Big\rbrace^{-1} \\ or \ [S][S]^{*t} &= [U] \end{aligned} \end{gather} $$
A Shift in Reference Planes
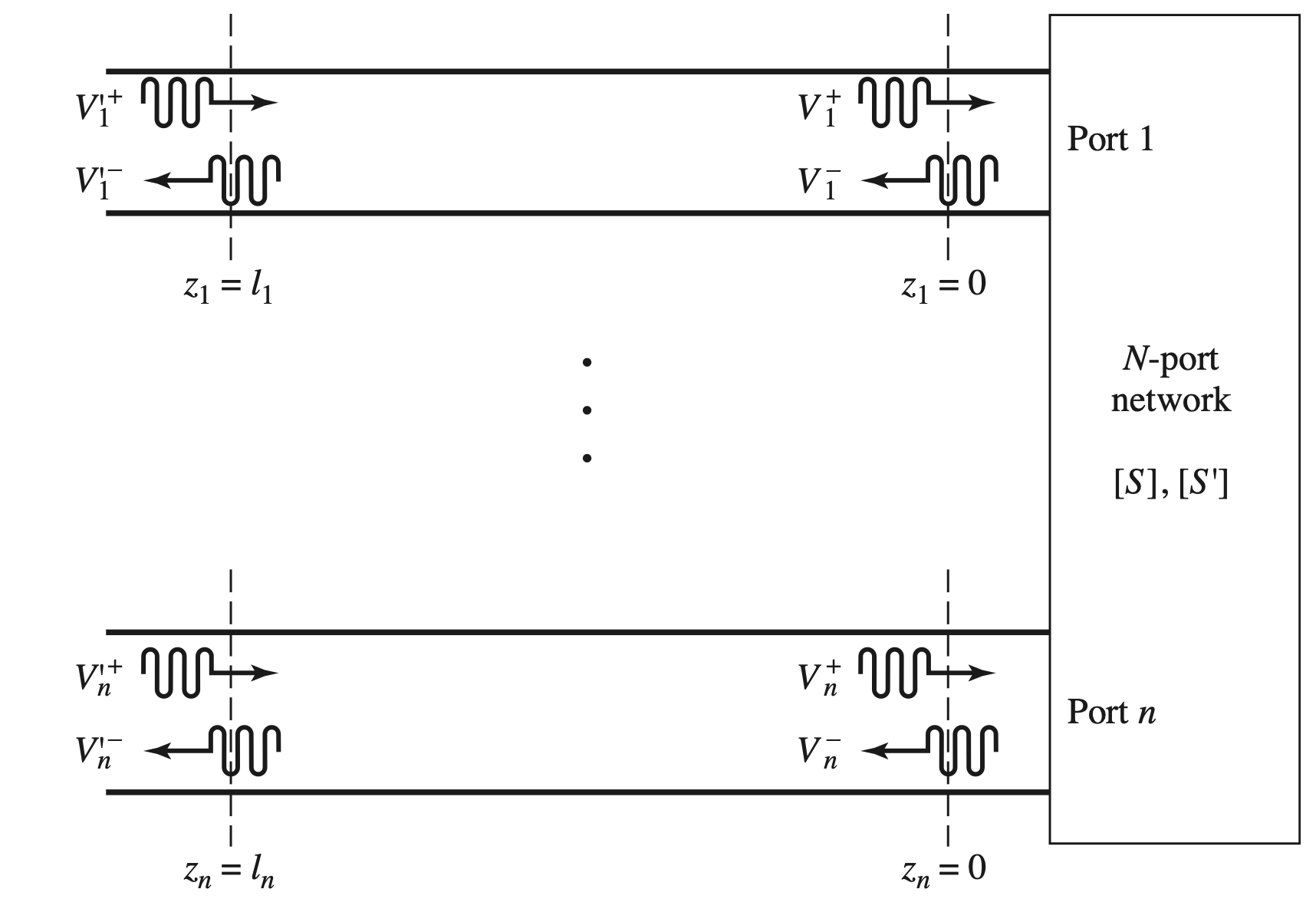
$$ \begin{gather} \begin{aligned} [V^-] &= [S] [V^+] \\ [V^-]’ &= [S]’ [V^+]’ \\ V_n^{-’} &= e^{-j \theta_n} V_n^- \\ V_n^{+’} &= e^{j \theta_n} V_n^+ \\ \theta_n &= \beta_n l_n \end{aligned} \end{gather} $$
- 化成矩阵形式
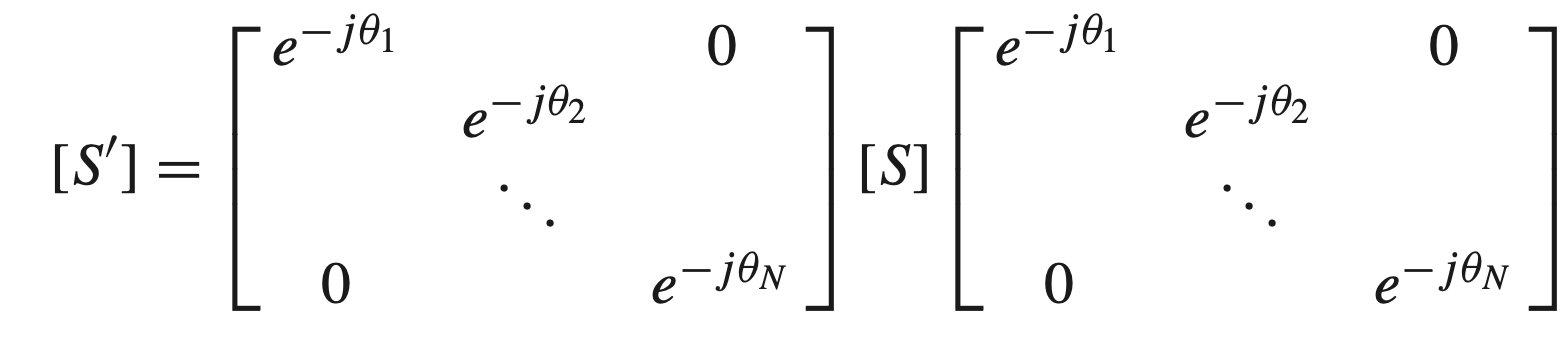
$$ \begin{gather} \begin{aligned} S_{nn}^{’} &= e^{-2j \theta_n} S_{nn} \end{aligned} \end{gather} $$
Power Wave & Generalized Scattering Parameters
Power Wave With Real Characteristic Impedance
$$ \begin{gather} \begin{aligned} P_L &= \frac{ 1 }{ 2 } \mathcal{Re} \Big\lbrace VI^* \Big\rbrace \\ &= \frac{ 1 }{ 2Z_0 } \mathcal{Re} \Big\lbrace (V_0^+ + V_0^-)(V_0^+ - V_0^-)^* \Big\rbrace \\ &= \frac{ 1 }{ 2 Z_0 } (|V_0^+|^2 - |V_0^-|^2) \end{aligned} \end{gather} $$
Power Wave With Complex Characteristic Impedance
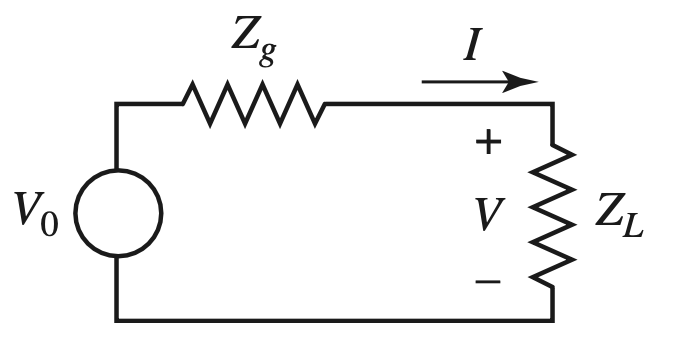
- 设立一个Reference Impedance $Z_R = R_R + j X_R$
$$ \begin{gather} \begin{aligned} a &= \frac{ V + IZ_R }{ 2 \sqrt{ R_R } } \\ b &= \frac{ V - IZ_R^* }{ 2 \sqrt{ R_R } } \\ V &= \frac{ Z_R^*a + Z_R b }{ \sqrt{ R_R } } \\ I &= \frac{ a-b }{ \sqrt{ R_R } } \end{aligned} \end{gather} $$
$$ \begin{gather} \begin{aligned} P_L &= \frac{ 1 }{ 2 } (|a|^2 - |b|^2) \\ \Gamma_P &= \frac{ b }{ a } = \frac{ Z_L - Z_R^* }{Z_L + Z_R } \end{aligned} \end{gather} $$
Transmission Matrix
Definition
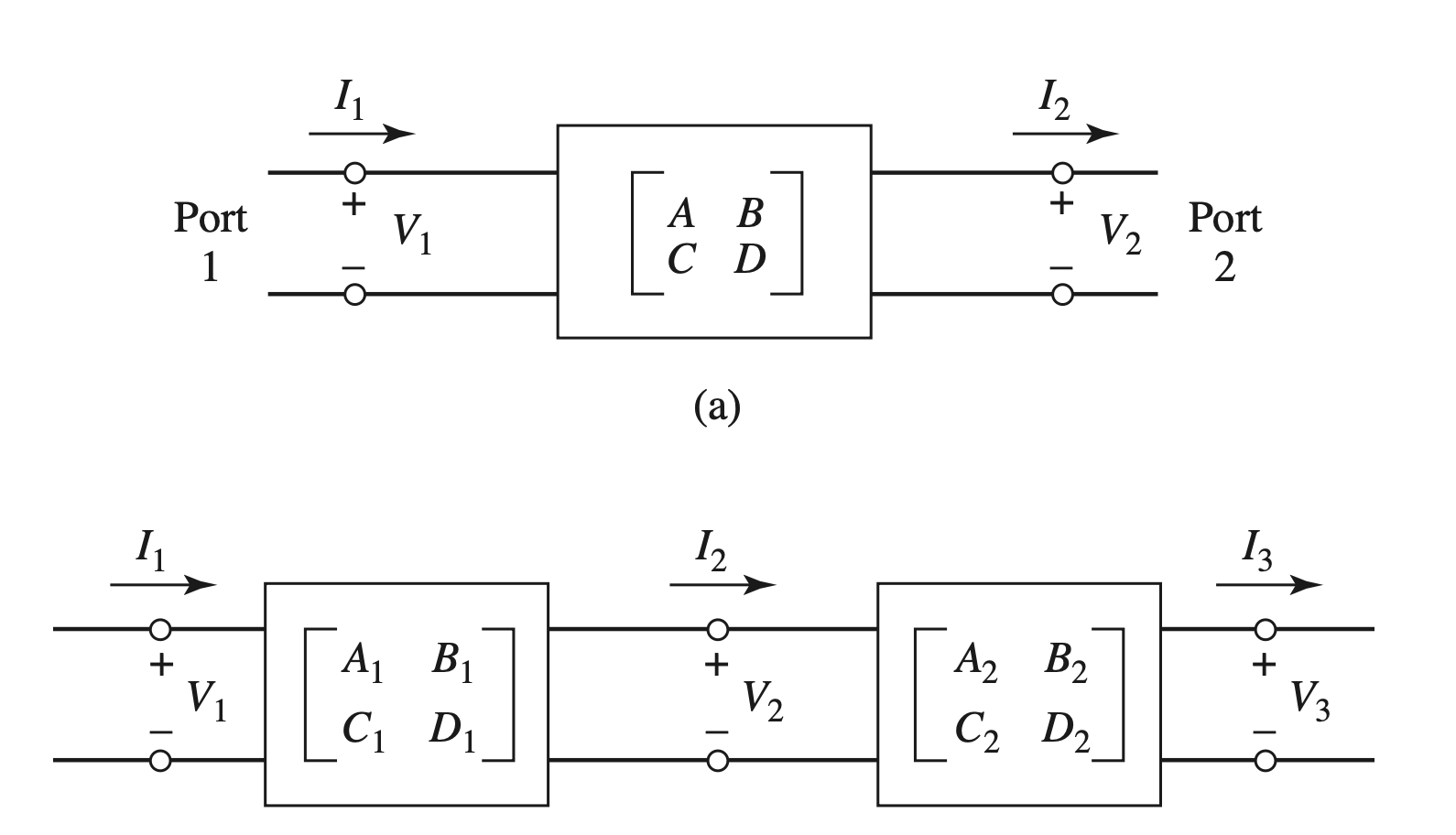
$$ \begin{gather} \begin{aligned} \begin{bmatrix} V_1 \\ I_1 \end{bmatrix} &= \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} V_2 \\ I_2 \end{bmatrix} \end{aligned} \end{gather} $$
常用电路结构的参数转化
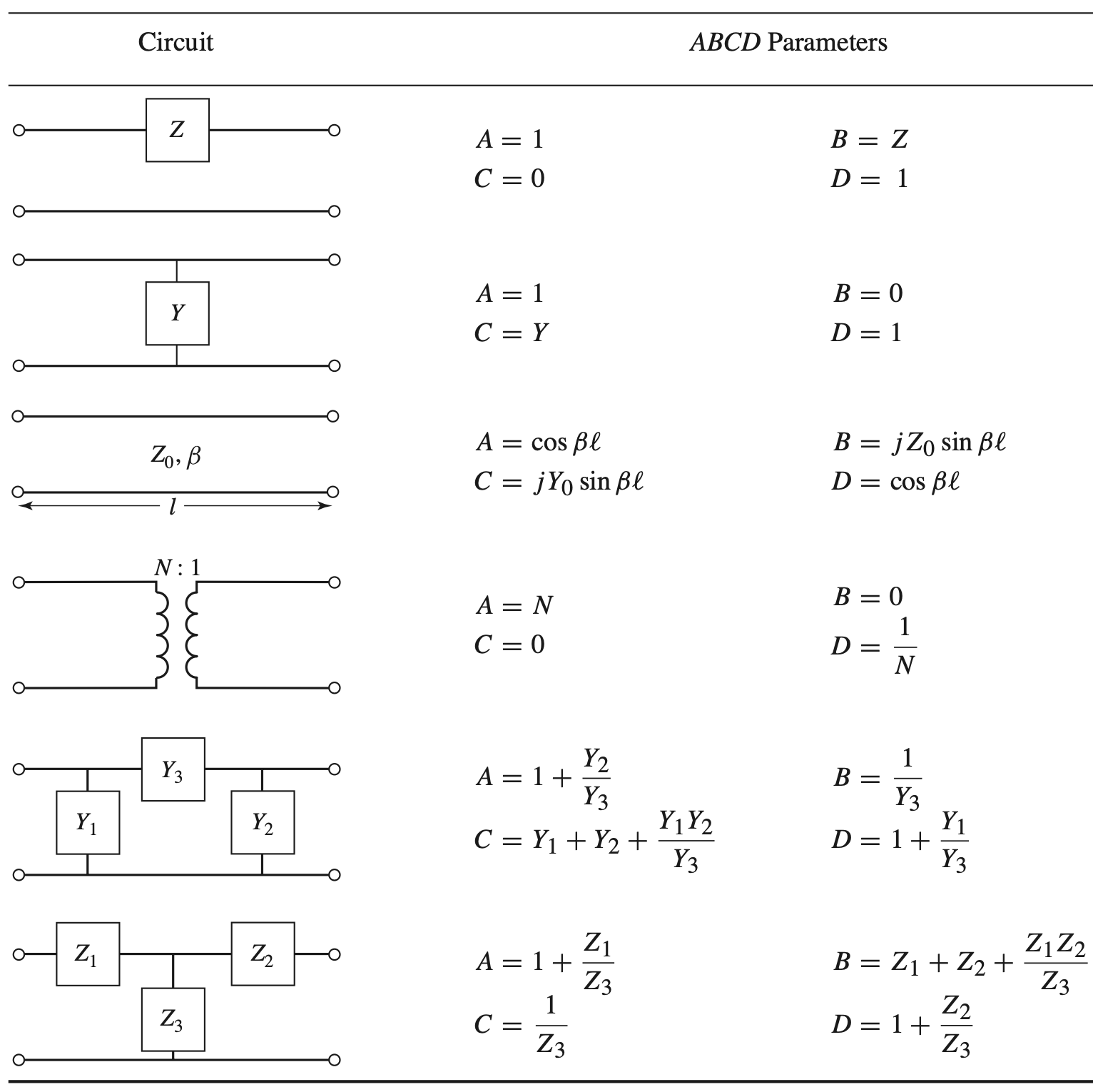
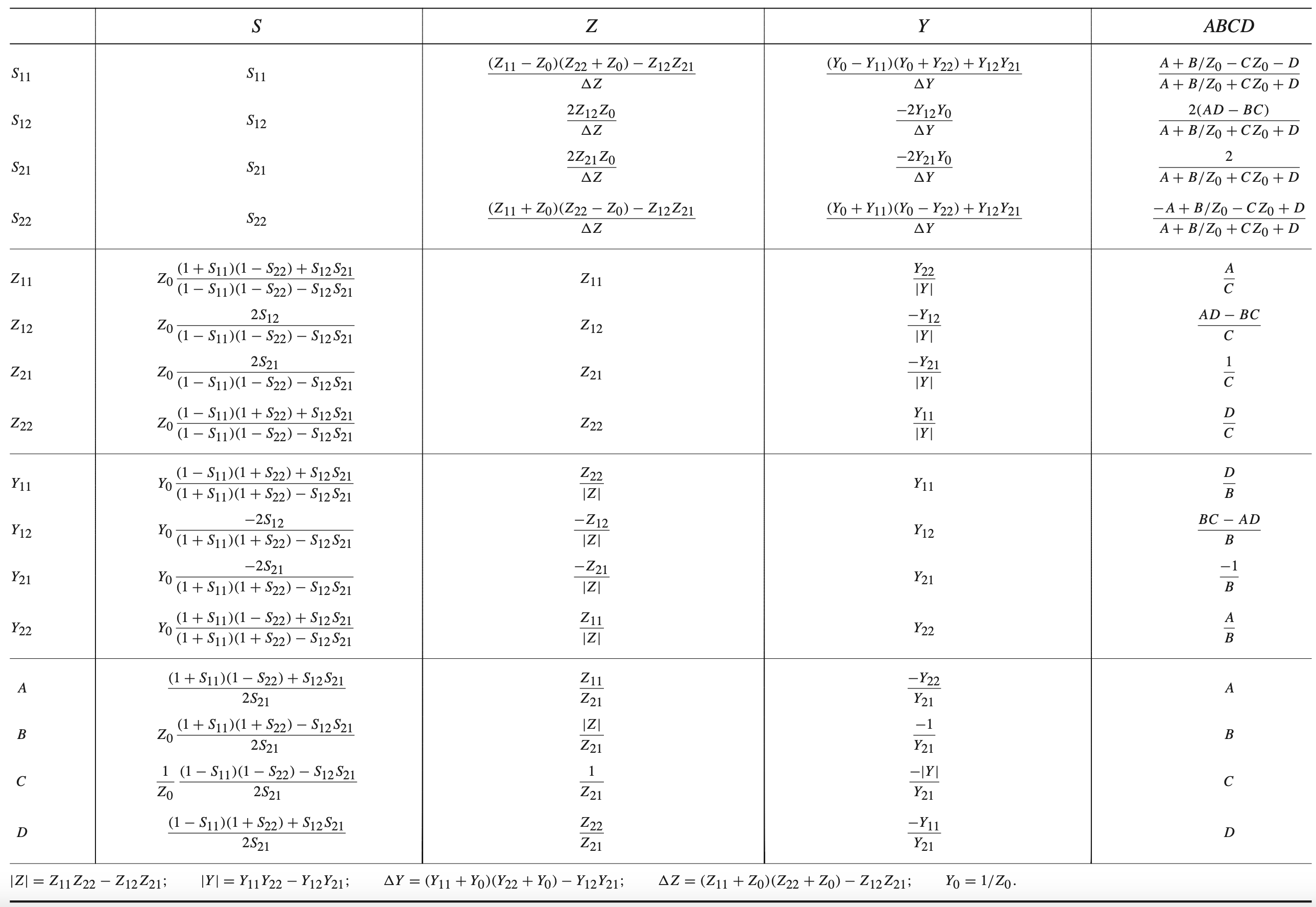
S Z Y ABCD Conversion (For 2-Port Network)
Signal Flow Graphs
Decomposition
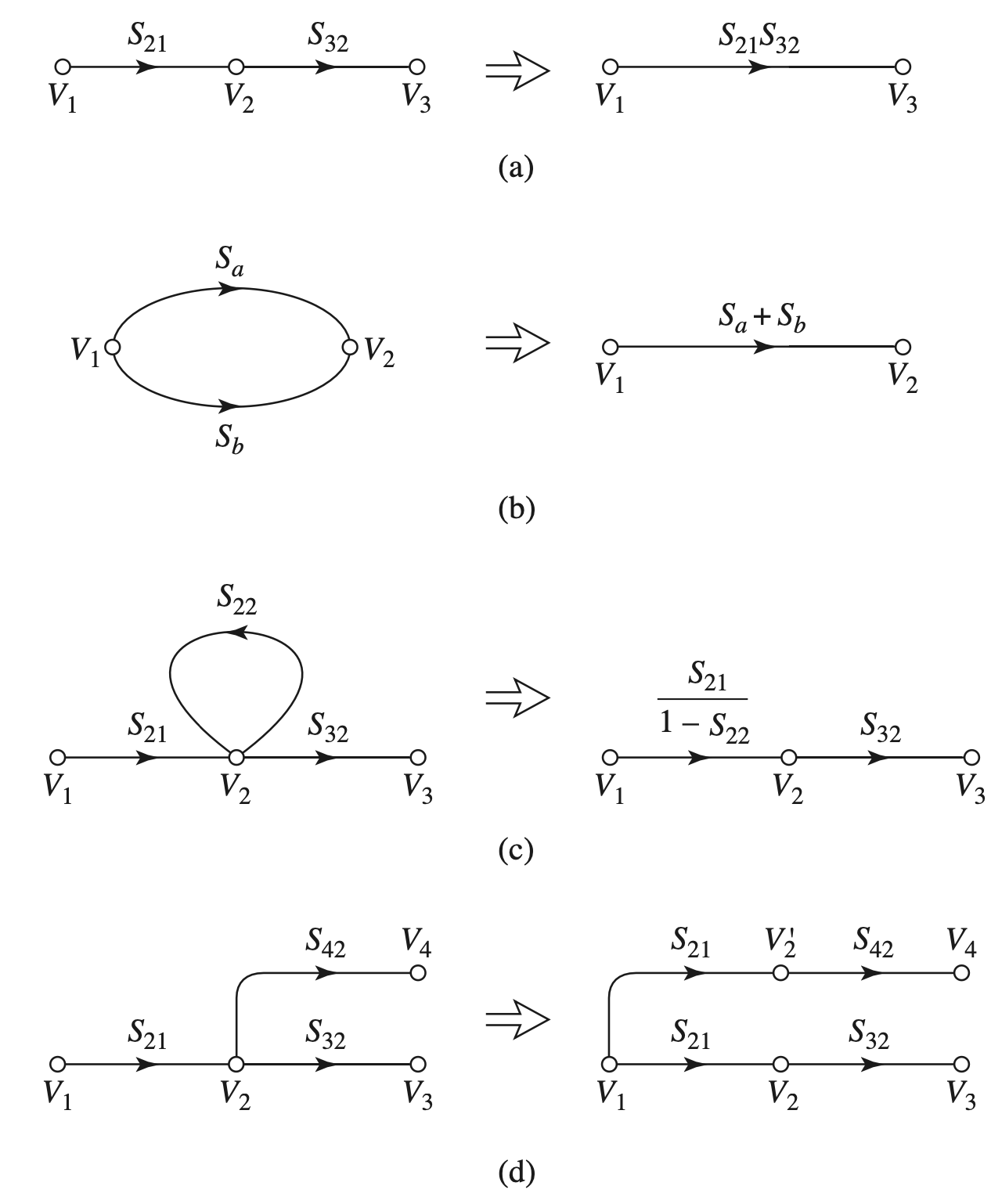
| Rules | Formula |
|---|---|
| Series Rule | $V_3 = S_{21}S_{32} V_1$ |
| Parallel Rule | $V_2 = (S_a + S_b) V_1$ |
| Self-Loop Rule | $V_3 = \dfrac{ S_{32} S_{21} }{ 1 - S_{22} }V_1$ |
| Splitting Rule | $V_4 = S_{42}S_{21} V_1$ |
Discontinuity & Modal Analysis
Discontinuity
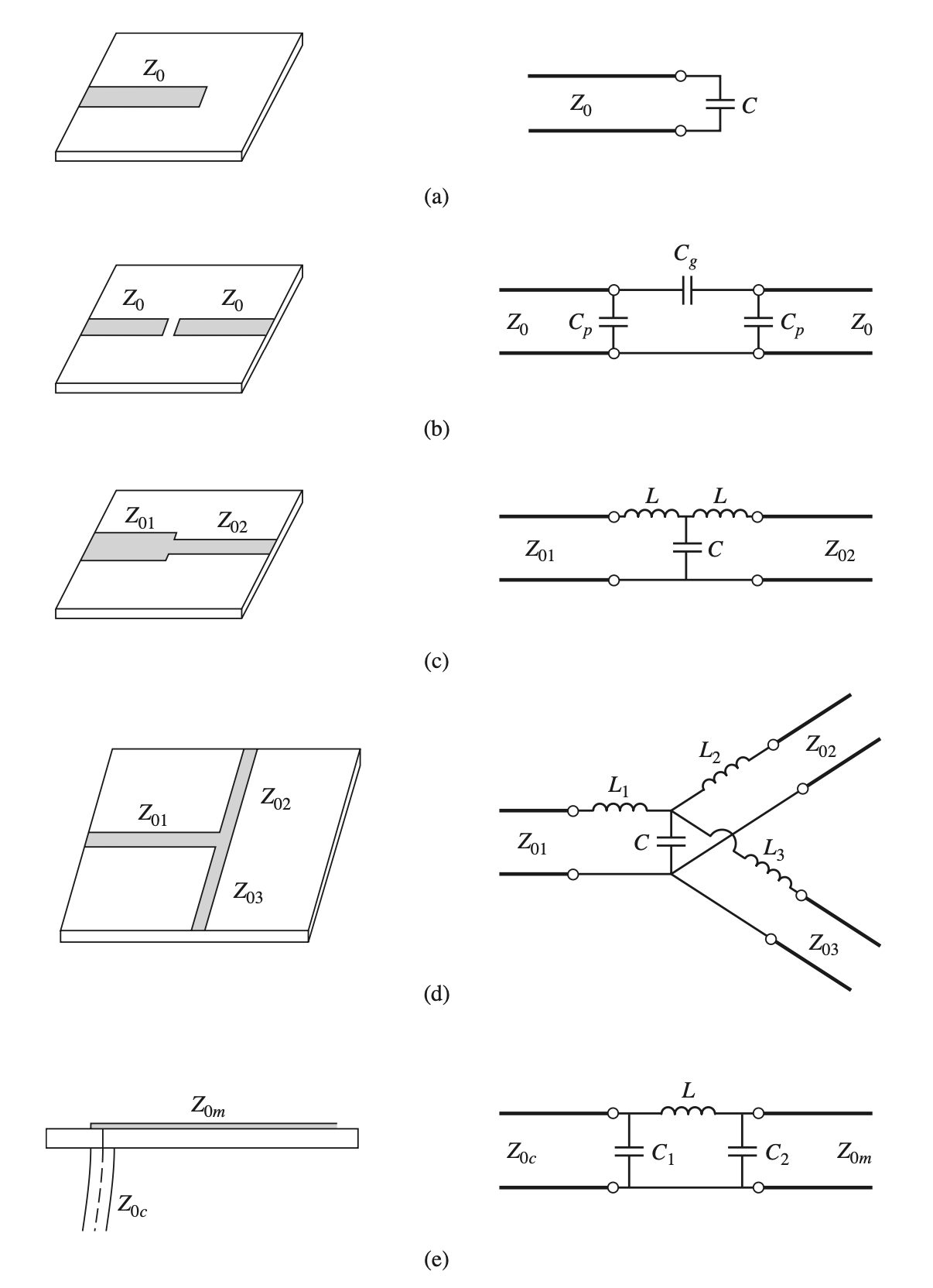
- Strip Line
- Microstrip Line