普朗克量子假设与光电效应

黑体

定义

黑体吸收一切照射其上的辐射

黑体辐射

黑体产生的辐射即为黑体辐射

Wien 定理 – – 仅在短波长时有效

• 光谱峰值处的波长$\lambda_p$ 与温度T的关系

$$ \lambda_p T = 2.90 \times 10^{-3} m\cdot K $$

不同温度下的黑体光谱

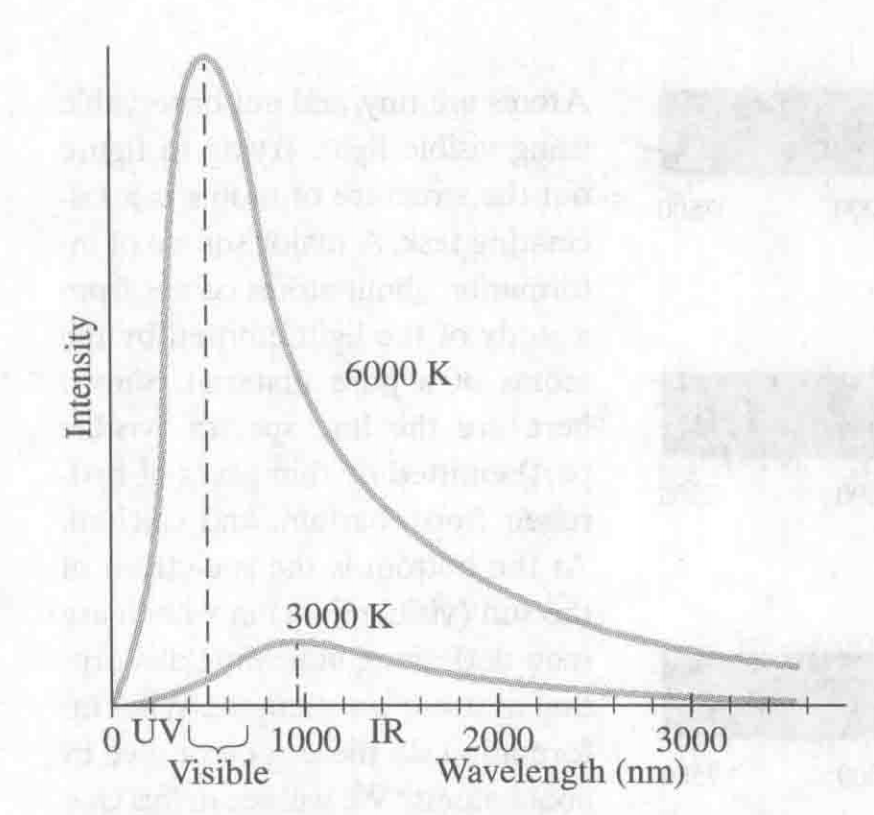
普朗克的工作

1. 前提

• Wien公式和Rayleigh等人的公式在波长较大时失效

2. 一定温度下光强与波长的公式 —— 普朗克辐射公式

$$ I(\lambda,T) = \frac{2\pi {h}c^2\lambda^{-5}}{e^{hc/\lambda k T}-1} \\\ \\ {h} = 6.626\times 10^{-34} \ J\cdot s \\\ \\ k \ \ Boltzman 常数 \\\ \\ T 在此处为给定的\pmb{常数} $$

3. 普朗克量子假设

• 能量是不连续的

$$ E = n{h}f, n=1,2,3,… $$

光电效应

图示

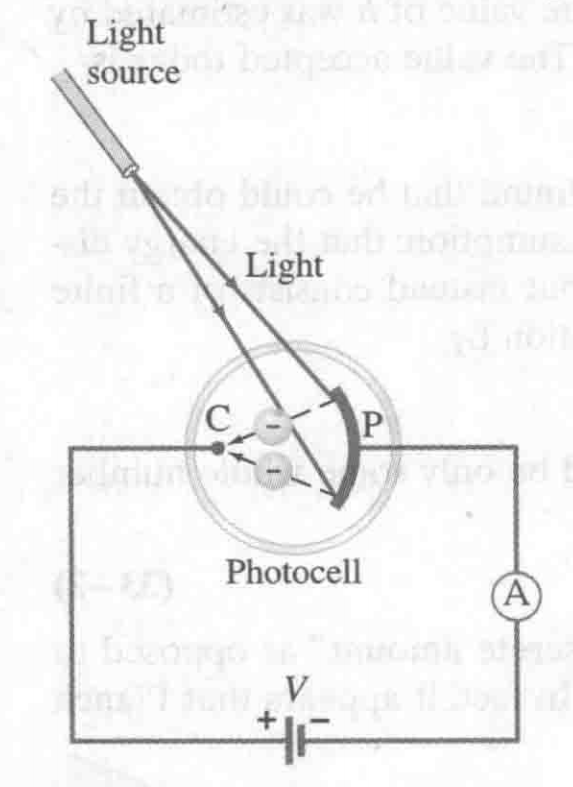
公式

$$ E_{k_{max}} = {h}f -W_0 \\\ \\ E_{k_{max}} = eV_0, f = \frac{c}{\lambda} $$

解释

1. 最大初动能$E_{kmax}$

• 光子和电子相撞，碰撞类型不同，损失的能量不同

康普顿效应 - 光子撞电子

光子动量

• 一般物质的动量为

$$ p = \gamma mv = \frac{mv}{\sqrt{1-v^2/c^2}} $$

• 光子的动量

由于光子的速度$v=c$，而其动量不可能为无穷，故其质量$m=0$

$$ E = mc^2 \longrightarrow E^2 = m^2 c^4 = p^2c^2 \\\ \\ \therefore \pmb{p =\frac{E}{c}} \\\ \\ p = \frac{{h}f}{c} = \frac{h}{\lambda} \\\ $$

康普顿效应与光子

2.2.1 实验图

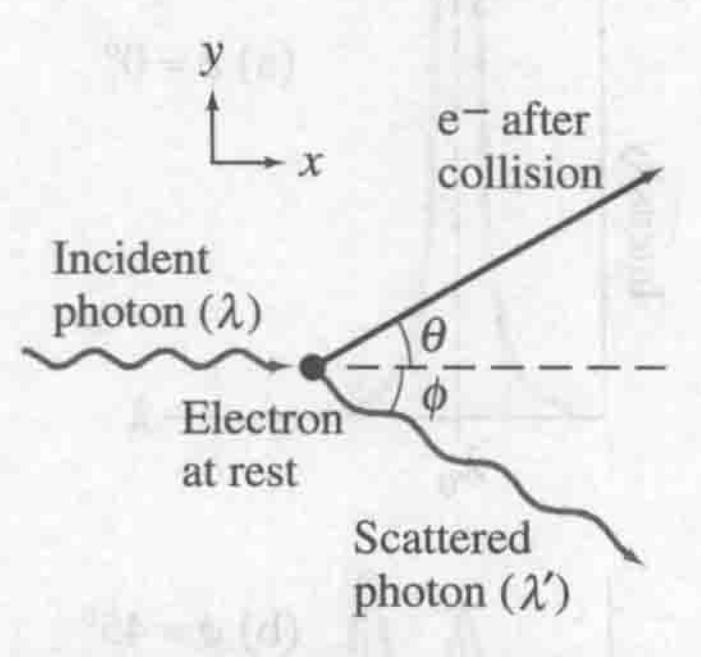
2.2.2 推导

$$ 已知: 撞前，电子静止，光子波长为\lambda; \\\ \\ 撞后，电子速率为v，光子波长为\lambda’ \\\ \\ 根据能量守恒有: \\\ \\ \begin{align} \frac{{h}c}{\lambda} = \frac{hc}{\lambda’} + (\frac{1}{\sqrt{1-v^2/c^2}}-1)m_e \end{align} \\\ \\ 根据动量守恒有: \\\ \\ \begin{align} \frac{m_ev}{\sqrt{1-v^2/c^2}}\cdot sin\theta = \frac{hc}{\lambda’}\cdot sin\phi \\ \frac{m_ev}{\sqrt{1-v^2/c^2}}\cdot cos\theta + \frac{hc}{\lambda’}\cdot cos\phi = \frac{hc}{\lambda} \end{align} \\\ \\ 根据上述三式: \\\ \\ \lambda’ =\lambda + \frac{{h}}{m_ec}(1-cos\phi) \\\ \\ \Delta E = h \nu - h\nu ’ = h\nu(1-cos\theta) \\\ \\ \pmb{Compton \ S{h}ift} \\\ \\ \Delta\lambda = \lambda’ - \lambda = \frac{{h}}{m_ec}(1-cos\phi) \\\ \\ \pmb{自由电子的康普顿波长} \\\ \\ \lambda_C = \frac{{h}}{m_ec} = 2.43\times 10^{-3}nm = 2.43pm $$

2.2.3 光子与原子的碰撞

1. 撞击原子核 或 核外电子。失去能量，频率降低(康普顿效应)

2. 撞击自由电子后消失,光电子逸出(光电效应)

3. 撞击核外电子后消失，电子能量增加(激发态)

4. 撞击后消失，产生电子和正电子(Pair Production)

• 这种情况下,正负电子对的动能为

$$ K = hf - 2mc^2 $$

2.2.4 光电效应与康普顿效应

光电效应是当光照在金属中时,金属里的自由电子由于变化的电场的作用而振动.若光振幅足够大,电子会飞出金属表面.于是金属就带了电.这个实验其实证明了光的波动性,即证明了光是一种电磁波.

康普顿效应是让光波射入石墨,企图让石墨中的电子对光进行散射,光子和电子碰撞时将一部分能量转移给电子.这样,光的能量减小,波长增加.而且如果将光子当作实物粒子的话,计算结果与实验结果符合.这便证明了光子也具有动量.即证明了光的粒子性.通常只发生在频率很高的电磁波当中

波粒二象性 互补原则

互补原理 —— 波尔

理解一个物理实验，必须使用波理论或者光理论，而不是同时使用两种理论

波粒二象性

光同时具有粒子和波的属性

$$ E(\pmb{粒子}的能量) = {h}f(\pmb{波}的频率) $$

物质的波属性

1. 德布罗意波

$$ 对于光，\because p = \frac{{h}}{\lambda} \\\ \\ 因此，\lambda = \frac{{h}}{p} $$

2. 解释

• 波的属性，例如干涉与衍射，只有在物体较小时才比较显著

早期原子模型

图示

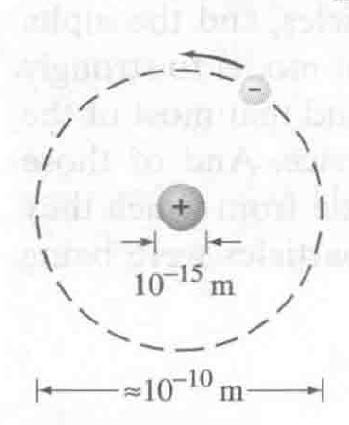
氢原子光谱

4.2.1 黑体辐射产生原因是

由原子和分子振动产生的

4.2.2 吸收光谱

1. 定义

连续光谱穿过稀有气体，产生的光谱中会有黑线，波长与稀有气体释放的相同，这叫吸收光谱

2. 结论

稀有气体吸收和释放的光的频率是相同的

4.2.3 Balmer公式

1. 适用范围

• 表示氢原子的发射(的光电子的)波长

$$ \frac{1}{\lambda} =R(\frac{1}{2^2}-\frac{1}{n^2})，n=3,4,5,… \\\ \\ Redberg常数 \ \ \ \pmb{R = 1.0974\times 10^7 m^{-1}} \\\ \\ 365nm \le \lambda \le 656nm $$

Balmer公式的延伸与图示

• Lyman Series

$$ \frac{1}{\lambda} =R(\frac{1}{1^2}-\frac{1}{n^2})，n=3,4,5,… \\\ \\ 91nm \le\lambda \le 122nm \\\ $$

• Paschen series

$$ \\ \frac{1}{\lambda} =R(\frac{1}{3^2}-\frac{1}{n^2})，n=3,4,5,… \\\ \\ 820nm\le \lambda \le 1280nm $$

• 氢原子能级图

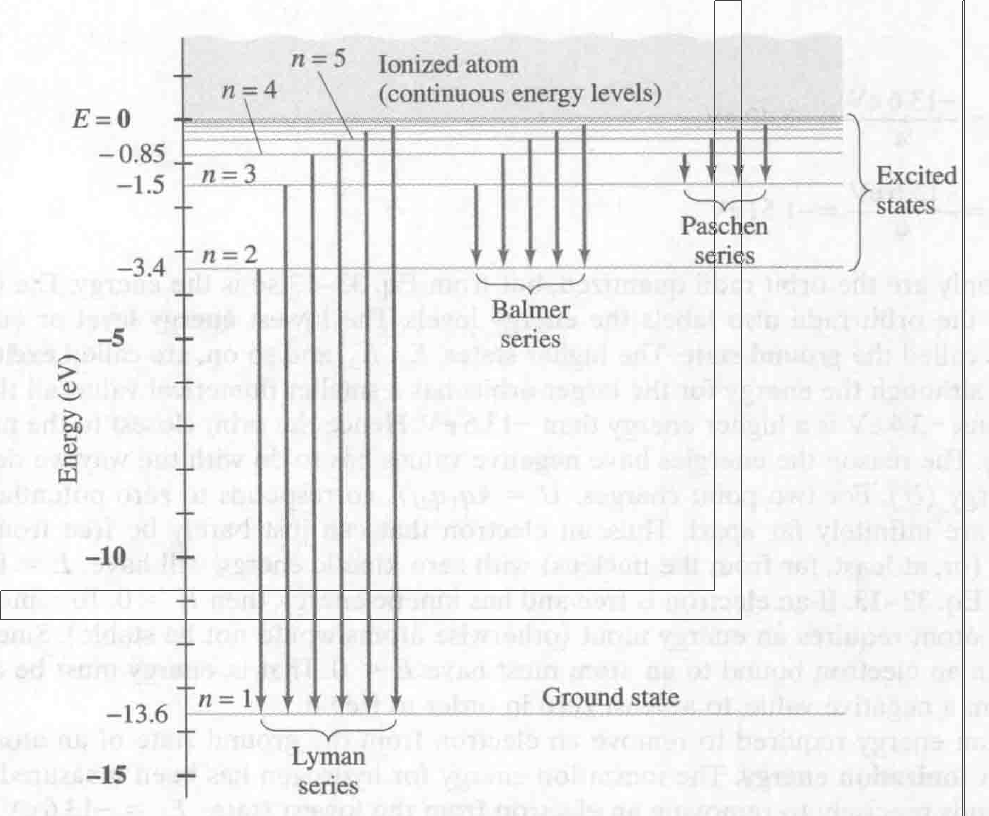
波尔模型

能级与跃迁

• 向低能级跃迁释放光子

$$ {h}f =E_u - E_l $$

波尔量子化条件

1. 条件

$$ 假设电子角动量 \ L = n \frac{{h}}{2\pi} \ \ \ \ n: 轨道的量子数 \\\ \\ 又 L =mvr_n \\\ \\ \therefore v = \frac{nh}{2\pi m r_n} (1) $$

• 波尔提出这个纯纯是因为它符合Balmer 公式，合着是瞎猜，一个一个试出来的

2. 验证

• 图示

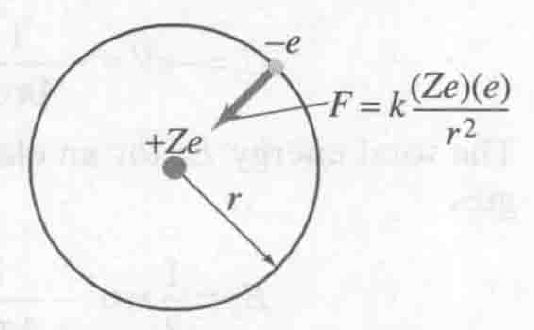
• 证明

$$ 根据牛顿第二定律 \\\ \\ F = ma \\\ \\ \frac{1}{4\pi \varepsilon_0} \frac{(Ze)(e)}{r^2_n} = m \frac{v^2}{r_n} \\\ \\ \therefore r_n = \frac{Ze^2}{4\pi \varepsilon_0 mv^2} \\\ \\ 又根据(1)式， v = \frac{nh}{2\pi r_n m} \\\ \\ \therefore \pmb{r_n = \frac{\varepsilon_0 n^2 h^2}{Ze^2 \pi m}} \\\ \\ \pmb {r_n = \frac{n^2}{Z} r_1} \\\ \\ 波尔半径 \ r_1 = \frac{\varepsilon_0 h^2}{\pi m e^2} = 0.529 \times 10^{-10}(m) = 0.0529(nm) $$

能级

1. 能级推导

$$ 核外电子的电势能U = - eV \\\ \\ U = -\frac{Ze^2}{4\pi \varepsilon_0 r_n} \\\ \\ 核外电子的总能量 E_n = E_k + E_p = \frac{1}{2}mv^2 -\frac{Ze^2}{4\pi \varepsilon_0 r_n} \\\ \\ 在波尔量子化条件下，v = \frac{n h}{2\pi m r_n } , r_n = \frac{\varepsilon_0 n^2 \hbar^2}{Ze^2 \pi m}\\\ \\ \therefore \pmb{E_n = -(\frac{Z^2e^4m}{8\varepsilon_0^2 h^2})(\frac{1}{n^2})} \\\ \\ \therefore \pmb{E_n = \frac{Z^2}{n^2}E_1} \\\ \\ 其中，E_1 = \frac{me^4}{8\varepsilon_0^2h^2} =-13.6eV $$

2. 关于能级解释

3. 其他概念

• 电离能/结合能：使核外电子从基态到脱离(自由到基态)原子核的最小能量

4. 能级与波长

$$ \frac{1}{\lambda} = \frac{f}{c} = \frac{hf}{hc} = \frac{1}{hc}(E_n - E_{n’}) \\\ \\ \lambda = \frac{hc}{E_n - E_{n’}} \\\ \\ 其中 \pmb{hc = 1.24 \times 10^3(eV\cdot nm)} \\\ \\ 换E \\\ \\ \frac{1}{\lambda} = \frac{Z^2e^4m}{8\varepsilon_0^2h^3 c}\Big(\frac{1}{n’^2}- \frac{1}{n^2}\Big) \\\ \\ 由此可以得到: R = \frac{me^4}{8\varepsilon_0 h^3 c} $$

德布罗意原子假设

对波尔量子化条件的证明（回顾驻波知识）

$$ 德布罗意波长 \lambda = \frac{h}{p} = \frac{h}{mv} (v较小时) \\\ \\ 2\pi r_n =n \lambda = n\frac{h}{mv}，n = 1,2,3, …\\\ \\ $$

波尔模型的局限性

1. 只适用于氢原子和单电子离子

2. 量子力学最终解释了这一切