探究氢原子中的量子数(Quantum Number)
主量子数(Principal)
$$ E_n = \frac{-13.6eV(E_1)}{n^2} \\\ \\ 此处的n即为主量子数 $$
轨道量子数(Orbital)
- 轨道量子数$l$与电子的轨道角动量的大小有关系
$$ L = \sqrt{l(l+1)}\hbar \\\ \\ \pmb{0 \le l \le (n-1)} $$
磁量子数(magnetic)
- 磁量子数表示轨道角动量的方向
$$ L_z = m_l \hbar \\\ \\ -l \le m_l \le l $$
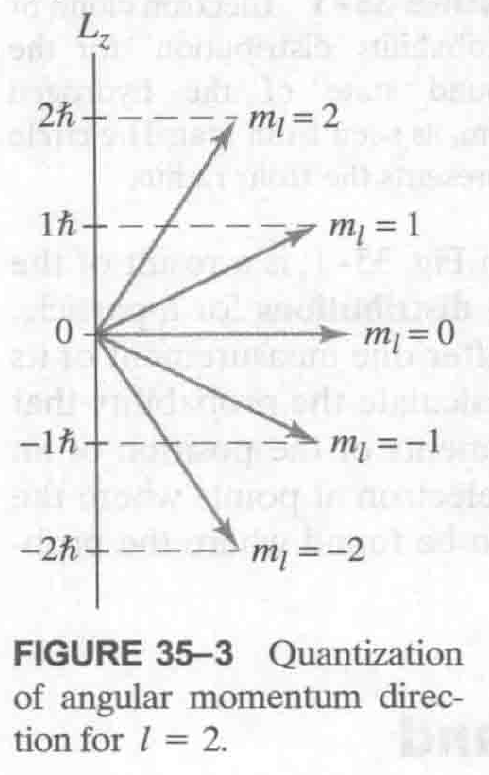
自旋量子数(spin)
- 自旋量子数表示自旋的方向
$$ m_s = +\frac{1}{2} \Leftrightarrow 上旋(Spin \ Up) \\\ \\ m_s = -\frac{1}{2} \Leftrightarrow 下旋(Spin \ Down) \\\ \\ 电子的自旋角动量S = \sqrt{s(s+1)}\hbar = \frac{\sqrt{3}}{2}\hbar $$
总结
- 在氢原子中,只有$n$影响能量
- 在其他原子中,$n$和$l$对电子能量的影响最大,$m_l$和$m_s$影响甚微
电子的跃迁
- Selection Rule
-
电子跃迁的轨道角动量变化只可能是$\Delta l = \pm 1$之间,
-
其他范围(包括$l=0$)叫做forbidden transition
氢原子波方程
基态氢原子薛定谔方程的解
$$ \psi_{100} = \frac{1}{\sqrt{\pi r_0^3}}e^{-\frac{r}{r_0}} \\\ \\ 其中, r_0 = \frac{h^2 \varepsilon_0}{\pi me^2} = 0.0529(nm),为\pmb{波尔半径} \\\ \\ \psi的下标分表表示n,l,m_l $$
氢原子中电子的概率分布
基态
$$ 假设P_r 是电子的半径分布概率,则 \\\ \\ P_rdr 可以看作电子分布在半径r处的概率 \\\ \\ 对于一个球壳来说,其体积 \\\ \\ dV = 4\pi r^2 dr \Longrightarrow |\psi|^2 dV = |\psi|^2 4\pi r^2 dr \\\ \\ \therefore P_r dr = |\psi|^2 dV \Longrightarrow P_r = 4\pi r^2 |\psi|^2 \\\ \\ 对于基态氢原子,P_r = 4\frac{r^2}{r_0^3}e^{-\frac{2r}{r_0}} $$
非基态的一些解
$$ \psi_{200} = \frac{1}{\sqrt{32\pi r_0^3}} (2-\frac{r}{r_0})e^{-\frac{r}{2r_0}} \\\ \\ P_{r200} = \frac{1}{8}\frac{r^2}{r_0^3}(2-\frac{r}{r_0})^2 e^{-\frac{r}{r_0}} \\\ \\ \psi_{210} = \frac{Z}{\sqrt{32\pi r_0^5}}e^{-r/2r_0} \\\ \\ \psi_{211} = \frac{x + iy}{\sqrt{64 \pi r_0^5}}e^{-r/2r_0} \\\ \\ \psi_{21-1} =\frac{x - iy}{\sqrt{64 \pi r_0^5}}e^{-r/2r_0} $$
元素周期表
泡利不相容原理
定义
每个轨道只能容纳两个电子,且自旋相反配对
- 即每个电子的四个量子数不可能完全相同
能量最低原理
原子的基态是能量最低的状态
洪特规则
电子分布到能量能级相同的轨道时,优先以自旋相同的方式分别占据不同的轨道
元素周期表
$Subshell$与$l$的关系
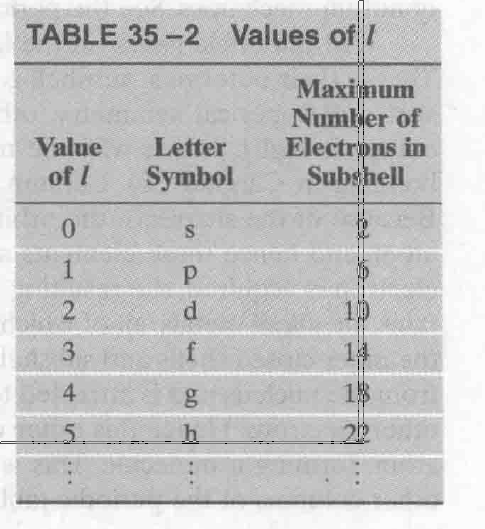
元素周期表

X射线和原子数
产生原因
由高能电子撞击X射线管道中的特定金属产生
X-射线 光强 —— 波长 关系图
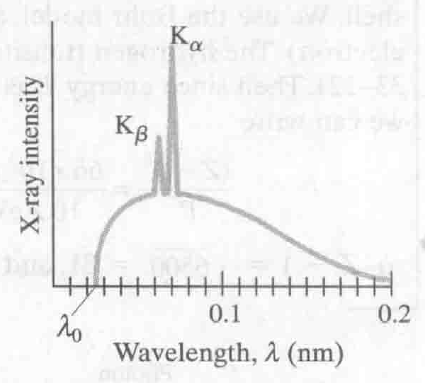
-
随着撞击电子的能量(即加速撞击电子的电压)增高,$\lambda_0$减小
-
$K_{\alpha}$和$K_{\beta}$两个峰体现了被撞击材料的特性,不因入射电子能量的改变而改变
关系
$$ 电子从n=2向n=1跃迁的过程中产生了K_{\alpha}\\\ \\ \lambda_{min} \propto \frac{1}{(Z-1)^2} \\\ \\ \lambda_{min}:最短的X射线 $$
电子与光子撞击过程中的能量转换
$$ E = hf_0 =eV \\\ \\ \therefore \lambda_0 =\frac{hc}{eV} $$
磁偶极矩 总角动量*
磁偶极矩
$$ \mu = IA = \frac{1}{2}evr \\\ \\ 又L = mvr \\\ \\ \therefore \mu = \frac{1}{2}\frac{e}{m}L \\\ \\ 由于电流中是电子(附点),所以磁偶极矩与角动量反向 \\\ \\ \begin{align} \therefore \pmb{\mu} = -\frac{1}{2}\frac{e}{m}\pmb{L} \\ U =- \pmb{\mu \cdot B} \end{align} \\ 假设B都在z方向上 \\\ \begin{align} 有 U = -\mu_z \cdot B_z \\ 又L_z = m_l\hbar \end{align} \\\ \\ 可以得到\mu = - \frac{e\hbar}{2m}m_l \\\ \\ 其中\mu_B = \frac{e\hbar}{2m} = 9.27 \times 10^{-24}(J/T),被称作\pmb{玻尔磁子} \\\ \\ 有 \mu = - \mu_B m_l $$