Nyquist Sampling Theorem

Impulse Train Sampling

$$ \begin{gather} \begin{aligned} p(t) &= \sum_{ n = - \infin }^{ \infin } \delta (t - n T) \\ x_p(t) &= x(t) p(t) \\ &= \sum_{ n = - \infin }^{ \infin } x(nT) \delta (t - n T) \\ X_P(j \omega) &= \frac{ 1 }{ 2 \pi } \int_{ - \infin }^{ \infin } X( j \omega) P ( j ( \omega - \theta)) d \theta \\ &= \frac{ 1 }{ T } \sum_{ n = - \infin }^{ \infin } X(j ( \omega - k \omega_s)) \\ \omega_s &= \frac{ 2 \pi }{ T} \end{aligned} \end{gather} $$

Nyquist Sampling Theorem

如果$X(j \omega ) = 0, \omega > | \omega_M |$, 那么对于$\omega_s > 2 | \omega_M|$, $x(t)$ 就唯一的由其样本$x(nT)$ 所确定, $2 \omega_M$ 被称作Nyquist Rate

Interpolation

Zero-Order Hold

下次采样之前保持住上次采样结果

Linear Interpolation (One-Order Hold)

将相邻采样点用直线连接

• 对于LPF

$$ \begin{gather} \begin{aligned} x_r(t) &= \sum_{ n = - \infin }^{ \infin } x(n T) \delta (t - nT) \\ &= \sum_{ n = - \infin }^{ \infin } x(nT) \frac{ \omega_c T }{ \pi } \frac{ sin ( \omega_c (t - nT)) }{ \omega_c (t - n T)} \end{aligned} \end{gather} $$

High-Order Hold

$\omega_c < 2\omega_M$, 信号重叠，发生 Under-Sampling

Reconstruction Filter

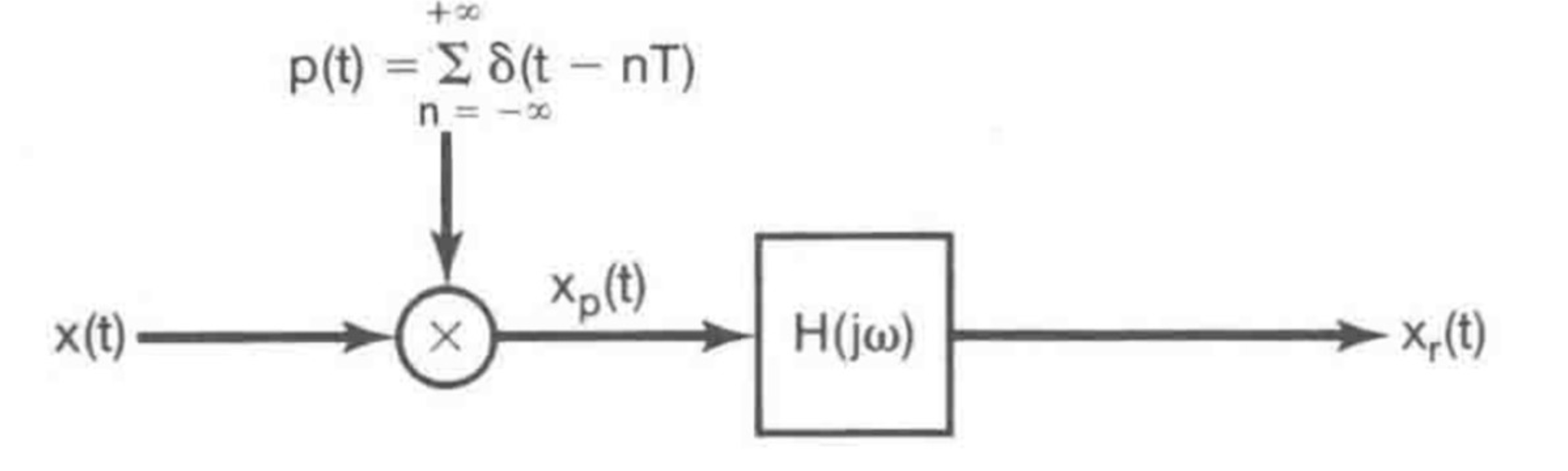
$$ \begin{gather} \begin{aligned} h(t) &= h_o(t) * h_r(t) \overset{ FT }{ \longleftrightarrow } H_o(j \omega) H_r(j \omega) = H(j \omega) \end{aligned} \end{gather} $$

D-T Processs for C-T Signals

Method

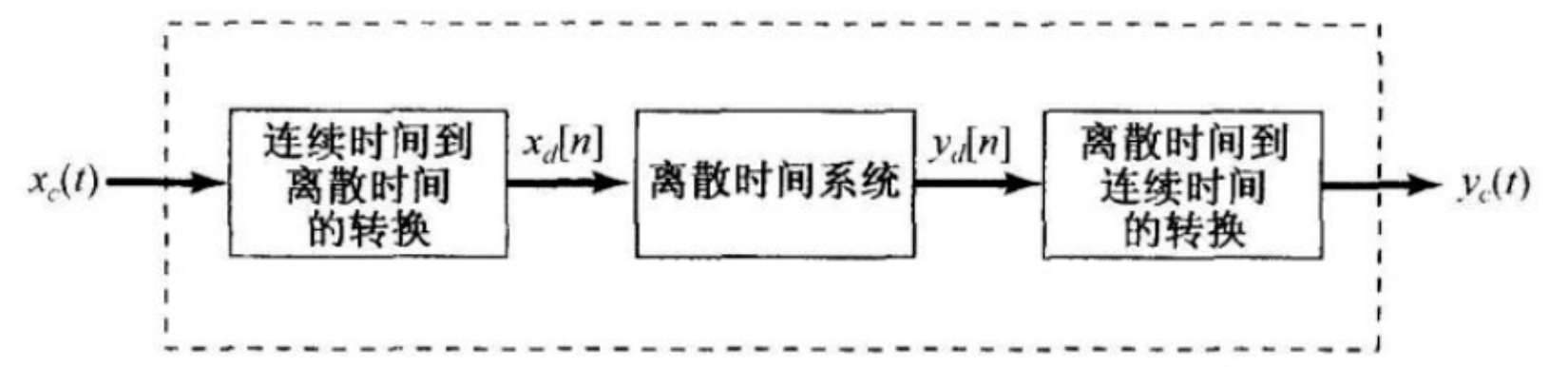
• 间隔从$T$变成$n$

$$ \begin{gather} \begin{aligned} x_d[n] &= x_c(t)* p(nT) \\ &= x_c(nT) \end{aligned} \end{gather} $$

几个傅立叶变换的关系

$$ \begin{aligned} x_c(t) &\overset{ FT }{ \longleftrightarrow } X_c(j \omega) \\ y_c(t) &\overset{ FT }{ \longleftrightarrow } Y_c(j \omega) \\ x_d[n] &\overset{ FT }{ \longleftrightarrow } X_d(e^{j \Omega}) \\ y_d[n] &\overset{ FT }{ \longleftrightarrow } Y_d(e^{j \Omega}) \end{aligned} $$

$$ \begin{gather} \begin{aligned} x_p(t) &= \sum_{ n = - \infin }^{ \infin } x_c(nT) \delta (t - nT) \overset{ FT }{ \longleftrightarrow } X_p (j \omega)= \sum_{ n = - \infin }^{ \infin } x_c(nT) e^{- j \omega nT} \\ X_d(e^{j \Omega}) &= \sum_{ n = - \infin }^{ \infin } x_d[n] e^{- j \Omega n} = \sum_{ - \infin }^{ \infin } x_c(n T) e^{-j \Omega n} \\ &= X_p(j \frac{ \Omega }{ T }) \\ &= \frac{ 1 }{ T } \sum_{ k = - \infin }^{ \infin } X_c(j \frac{ \Omega - 2 \pi k }{ T }) \end{aligned} \end{gather} $$

Filtering

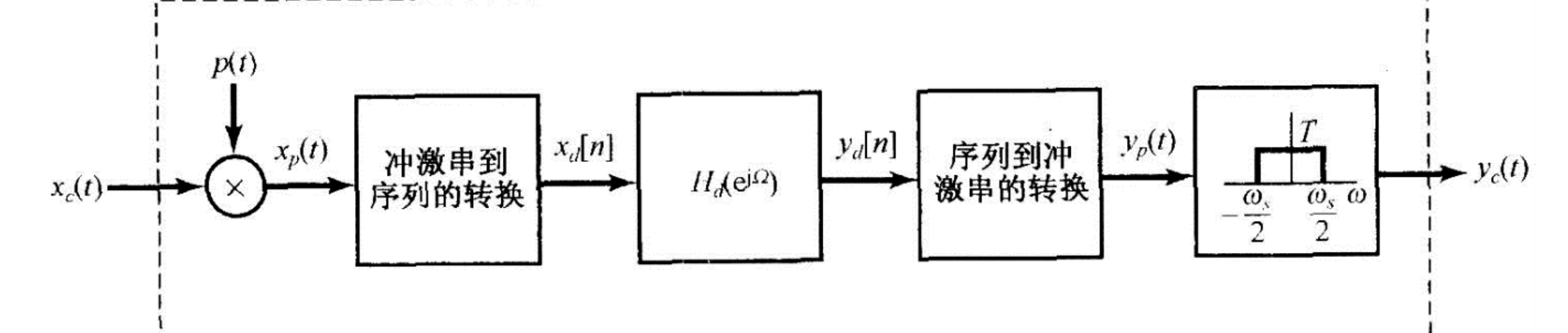
Complex Expotential & Sinusoidal Modulation

Complex Expotential Modulation

Modulation & Fourier Transfer

$$ \begin{gather} \begin{aligned} c(t) &= e^{j( \omega_c t + \theta_c)} \\ y(t) &= x(t) c(t) \end{aligned} \end{gather} $$

$$ \begin{gather} \begin{aligned} Y(j \omega) &= \frac{ 1 }{ 2\pi } \int_{ - \infin }^{ \infin } X(j \theta) C(j( \theta - \omega)) d \theta \\ C(j \omega) &= 2\pi \delta ( \omega - \omega_c) \\ Y(j \omega) &= X(j \omega - j \omega_c) \end{aligned} \end{gather} $$

Modulation & Demodulation

• 如果 $\theta_c = 0$

$$ \begin{gather} \begin{aligned} y(t) &= x(t) e^{j \omega_c t} \\ x(t) &= y(t) e^{-j \omega_c t} \end{aligned} \end{gather} $$

Sinusoidal Modulation

$$ \begin{gather} \begin{aligned} c(t) &= cos( \omega_c t + \theta_c) \\ c(j \omega) &= \pi [ \delta ( \omega - \omega_c) + \delta ( \omega + \omega_c)] \\ Y(j \omega) &= \frac{ 1 }{ 2 } [ X(j \omega - j \omega_c) + X(j \omega + j \omega_c)] \\ \end{aligned} \end{gather} $$

Sinusoidal Amplitude Demodulation

Sync Demodulation

In Phase

$$ \begin{gather} \begin{aligned} y(t) &= x(t) cos( \omega_c t) \\ w(t) &= y(t) cos(- \omega_c t) \\ &= x(t) cos^2( \omega_c t) \\ &= \frac{ 1 }{ 2 } x(t) + \frac{ 1 }{ 2 } x(t)cos(2 \omega_c t) \end{aligned} \end{gather} $$

Out of Phase

1. For Complex Signals

$$ \begin{gather} \begin{aligned} y(t) &= e^{j ( \omega_c t+ \theta_c)} x(t) \\ w(t) &= e^{-j ( \omega_c t + \phi_c)} y(t) \\ &= e^{j ( \theta_c - \phi_c)} x(t) \end{aligned} \end{gather} $$

2. For Sinusoidal Signals

$$ \begin{gather} \begin{aligned} w(t) &= cos( \omega_c t + \theta_c) cos( \omega_c t + \phi_c) x(t) \\ &= \frac{ 1 }{ 2 } cos( \theta_c - \phi_c) x(t) + \frac{ 1 }{2 } cos( 2 \omega_c t + \phi_c + \theta_c) \end{aligned} \end{gather} $$

Async

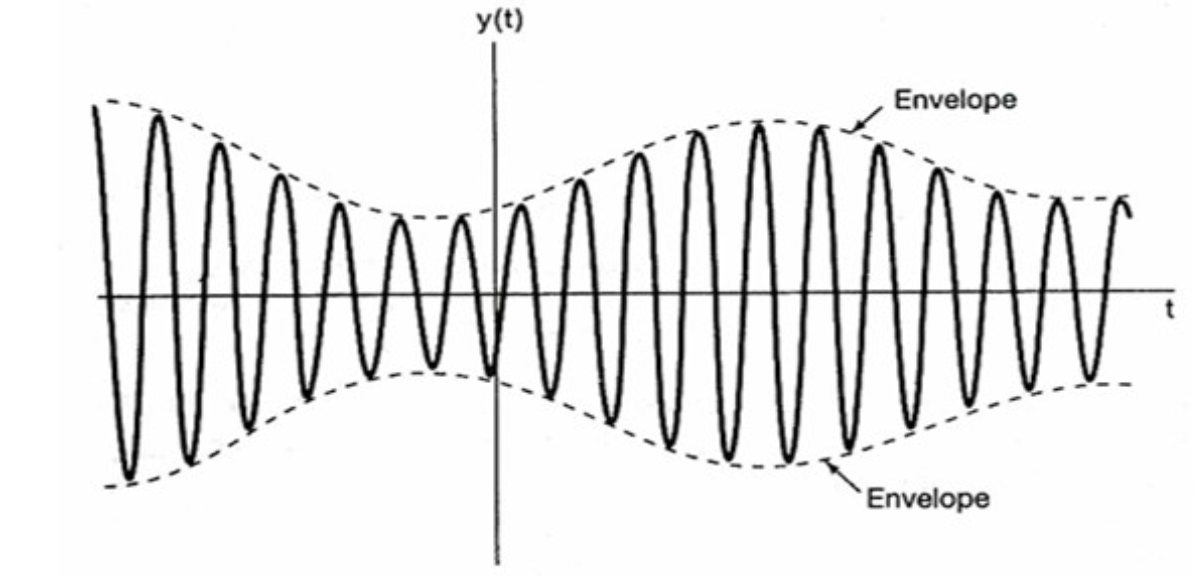
• $x(t)$总是正的

$$ \begin{gather} \begin{aligned} y(t) &= x(t) + A \\ |x(t)| &\le K \\ A &\ge K \\ m &= \frac{ K }{A} \end{aligned} \end{gather} $$

• $m$越大，信号质量越好