海森堡不确定性原理

内容

一个物体的动量和它的位置不可能被同时准确地观测到

解释

1. 原理

• 需要用光子撞击电子才能知道它的位置,而撞击会增加电子的动量，改变其位置

2. 根据$p = \frac{h}{\lambda}$

• 波长越大，动量越大，动量测不准，位置也会改变

• 波长越小，动量太小，仪器没法精确测量，位置不准

公式

1. 动量和位置

$$ 对于波长为\lambda的光子 \\\ \\ \Delta x \approx \lambda \\\ \\ \Delta p \approx \frac{h}{\lambda} \\\ \\ \therefore (\Delta x)(\Delta p) \approx h \\\ \\ 根据海森堡的精确计算(这课本真省事) \\\ \\ (\Delta x)(\Delta p) \ge \frac{h}{2\pi} $$

2. 能量与时间

$$ \Delta E = hf = \frac{hc}{\lambda} \\\ \\ \Delta t \approx \frac{\lambda}{c} \\\ \\ (\Delta E )(\Delta t) = h \\\ \\ (\Delta E )(\Delta t) \ge \frac{h}{2\pi} \\\ \\ 科学家们给这个常用的量换了个名字: \ \hbar = \frac{h}{2\pi} $$

一维薛定谔方程时间无关形式

不考虑时间

$$ 假设\psi(x) = Asinkx + Bcoskx \\\ \\ k = \frac{2\pi}{\lambda} = \frac{2\pi p}{h} = \frac{p}{\hbar} (1)\\\ \\ \frac{d^2\psi(x)}{dx^2} = -k^2 \varphi(x) (2)\\\ \\ 根据能量守恒 \\\ \\ K + U = E \ \ \ \ 动能 + 势能 = 总能量 \\\ \\ \frac{p^2}{2m} + U = E (3)\\\ \\ 根据(1)式 ， p = k\hbar \\\ \\ \therefore \frac{k^2\hbar^2}{2m} + U =E (4)\\\ \\ 结合(2)和(3)式，-\frac{\hbar^2}{2m} \frac{d^2\psi(x)}{dx^2} = \frac{\hbar^2k^2}{2m}\varphi(x) \\\ \\ 对(4)式两端乘以\psi(x),得到\pmb{一维薛定谔方程的无时间形式} \\\ \\ -\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2} + U(x) \cdot \varphi(x) = E\cdot \varphi(x) $$

三维形式

将上式的$(x)$改为$(x,y,z)$即可

一维形式的正交化条件

$$ \int_{三维} |\psi|^2dV = \int_{一维} |\varphi|^2dx = 1 $$

薛定谔方程的时间有关形式

公式

$$ \frac{\hbar^2}{2m}\frac{\partial^2 \psi(x,t)}{\partial x^2} + U(x) \cdot \psi(x,t) = i\hbar \frac{\partial \psi(x,t)}{\partial t} \\\ \\ 很多时候， \psi(x,t) = \varphi(x)\cdot f(t)\\\ \\ \therefore -\frac{\hbar}{2m} \frac{d\varphi^2(x)}{dx^2}\cdot f(t) + U(x) \cdot \varphi(x)\cdot f(t) = i\hbar \frac{df(t)}{dt}\varphi(x) \\\ \\ 两边同时除以f(t)\cdot \varphi(x) \\\ \\ -\frac{\hbar}{2m}\frac{1}{\varphi(x)} \frac{d\varphi^2(x)}{dx^2} + U(x) = i\hbar \frac{1}{f(t)} \frac{df(t)}{dt} = C \\\ \\ 对于上式，两边分别只有一个变量 \\\ \\ 故分别让两边等于同一个常数即可 \\\ \\ -\frac{\hbar}{2m} \frac{d^2\varphi(x)}{dx^2} +U(x) \varphi(x) = C\varphi(x) \\\ \\ 注意到，上式与时间无关的以为薛定谔方程相同 \\\ \\ \therefore C = E \\\ \\ \therefore i\hbar \frac{1}{f(t)} \frac{df(t)}{dt} = E \\\ \\ \therefore \frac{df(t)}{dt} = -i\frac{f(t)}{\hbar} E \\\ \\ 解得：f(t) = e^{-i(\frac{E}{\hbar})t} \\\ $$

波的方程

$$ \psi(x,t) =\varphi(x) e^{-i(\frac{E}{\hbar})t}\\\ \\ 根据欧拉公式：|f(t)| =1 \Longrightarrow |f(t)|^2 = 1 \\\ \\ \therefore |\psi(x,t)|^2 = |\varphi(x)|^2 $$

自由粒子 平面波 波包

自由粒子

• 不受任何外力的粒子, 其势能为0

自由粒子的薛定谔方程

$$ \frac{d^2\psi(x)}{dx^2} + \frac{2mE}{\hbar^2}\psi(x) = 0 \\\ \\ 其中, k =\frac{2\pi}{\lambda} = \frac{p}{\hbar} = \sqrt{\frac{2mE}{\hbar^2}} $$

粒子在无限深的井中的势能

图示

$$ 我们规定 \\\ \\ U(x) = \begin{cases} 0 & 0 \lt x \lt L \\ \infin & x \le 0 \ or \ x \ge L \end{cases} $$

波方程

$$ 当x \lt 0 \ or \ x \gt L ，U(x) = \infin \\\ \\ 为了使得薛定谔方程成立，U(x) \cdot \psi(x)= 0 \\\ \\ \therefore \psi(x) =0 \\\ \\ 我们认为一个波函数是\pmb{连续的} \\\ \\ \therefore 当x= 0和x = L 时，\psi(x) = 0 \\\ \\ \psi(0) = B = 0\\\ \\ \psi(L) = A\cdot sinkL = 0 \\\ \\ \therefore k = \frac{n\pi}{L} \\\ \\ \therefore \psi_n(x) = Asin\frac{n \pi}{L}x\\\ \\ 根据归一化条件 \\\ \\ \int_{0}^{L} |\psi(x)|^2dx = 1 \\\ \\ 解得: A = \sqrt{\frac{2}{L}} \\\ \\ \therefore \psi_n(x) =\sqrt{\frac{2}{L}}sin\frac{n\pi}{L}x $$

能量方程

1. 方程

$$ \because k = \sqrt{\frac{2mE}{\hbar^2}} \\\ \\ E_n = \frac{k^2\hbar^2}{2m} = n^2 \frac{h^2}{8mL^2} \\\ \\ \therefore E_1 =\frac{h^2}{8mL^2},\pmb{零点能量} $$

2. 观察与解释

$$ p = \frac{h}{\lambda} = \hbar k = n\hbar\frac{\pi}{L} \\\ \\ p与L 成反比 $$

• 这可以理解为不确定性原理的一种体现

粒子在有限深井中的势能

图示

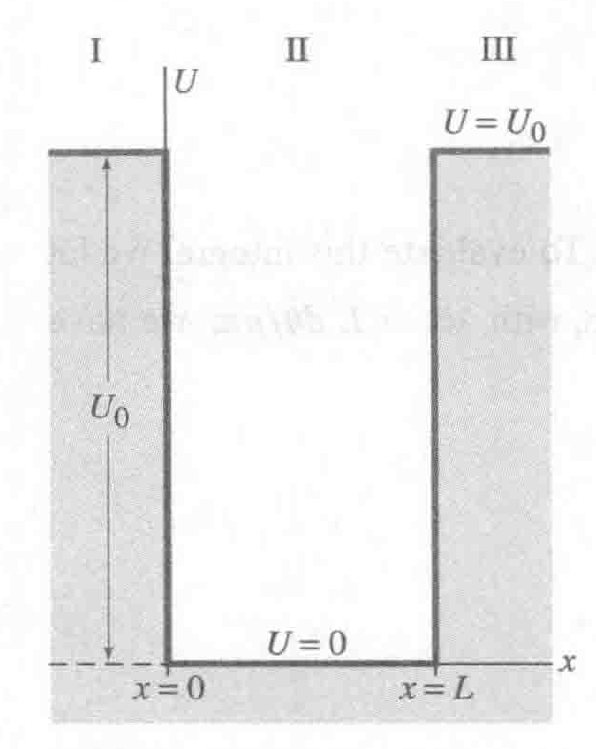
波方程

$$ 设 \psi = Asinkx + Bcoskx \\\ \\ -\frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} + U\psi = E\psi \\\ \\ \frac{d^2\psi}{dx^2} - \Big[\frac{2m(U_0 -E)}{\hbar^2}\Big] \psi = 0 \\\ \\ 设G^2 = \frac{2m(U_0-E)}{\hbar^2} \\\ \\ \pmb{当U_0 \gt E}时: \\\ \\ \psi_{I,III} = Ce^{Gx} + De^{-Gx} \\\ \\ 在I处，x \lt 0 \Longrightarrow 当x \rightarrow -\infin 时, \psi \rightarrow +\infin \\\ \\ 这显然不可能，故D = 0 \\\ \\ 同理，在III处，C = 0 \\\ \\ 我们得到 \begin{cases} \psi_I = Ce^{Gx} \\ \psi_{III} = De^{-Gx} \end{cases} \\\ \\ 由于波方程是连续且可微的 \\\ \\ 故有x =0 时: \psi_I = \psi_{II}，\frac{d\psi_I}{dx} = \frac{d\psi_{II}}{dx} \\\ \\ x= L时: \psi_{II} = \psi_{III} ，\frac{d\psi_{II}}{dx} = \frac{d\psi_{III}}{dx} \\\ \\ 解得 \pmb{B = C， GC = kA} $$

另一种情况

$$ 当U_0 \lt E \\\ \\ 我们有 \lambda =\begin{cases} \frac{h}{p} = \frac{h}{\sqrt{2mE}} & 0 \le x \le L \\ \frac{h}{p} = \frac{h}{\sqrt{2m(E-U_0)}} & x\gt L \ or \ x \lt 0 \end{cases} \\\ $$

穿越障碍

图示

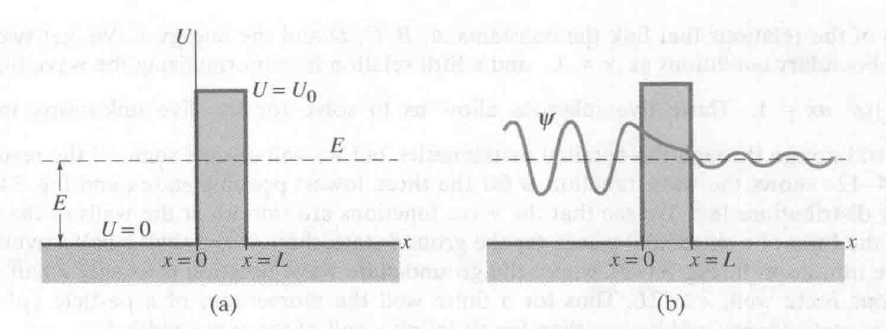
解释

1. 前提：$U_0 \gt E$

2. 有一部分粒子会穿过障碍，如图(b)所示

$$ 假设穿过概率为T,反弹概率为R,有T+R = 1 \\\ \\ 当T 非常小时 \\\ \\ T = \frac{|\psi(L)|^2}{|\psi(0)|^2} = e^{-2GL} $$