Basic Properties of PD & DP

3-Port Network

• 三端口网络不可能同时满足Reciprocal, Lossless, Matched

$$ \begin{gather} \begin{aligned} [S] &= \begin{bmatrix} 0 & S_{12} & S_{13} \\ S_{12} & 0 & S_{23} \\ S_{13} & S_{23} & 0 \end{bmatrix} \\ [S]^t[S]’ &= [U] \end{aligned} \end{gather} $$

4-Port Network

Reciprocal & Matched & Lossless

1. Reciprocal & Matched

$$ \begin{gather} \begin{aligned} [S] &= \begin{bmatrix} 0 & S_{12} & S_{13} & S_{14} \\ S_{12} & 0 & S_{23} & S_{24} \\ S_{13} & S_{23} & 0 & S_{34} \\ S_{14} & S_{24} & S_{34} & 0 \end{bmatrix} \end{aligned} \end{gather} $$

2. Lossless

• 根据Unitary Matrix的性质, 分别将Row(12,34,13,24)相乘，然后相减

$$ \begin{gather} \begin{aligned} [S]^t [S]’ &= 0 \\ S_{13} S_{23}’ + S_{14} S_{24}’ &= 0 \\ S_{13} S_{14}’ + S_{23} S_{24}’ &= 0 \\ S_{13} (S_{23}’ - S_{14}’) + S_{24}’(S_{14} - S_{23}) &= 0 \\ S_{12} (S_{24}’ - S_{13}’) + S_{34}’(S_{13} - S_{24}) &= 0 \end{aligned} \end{gather} $$

Solution

Solution I

1. 以上方程的一个可能解是$S_{23} = S_{14} = 0$

• 基于这个解，再次利用Unitary Matrix的定义可以得到

$$ \begin{gather} \begin{aligned} |S_{12}|^2 + |S_{13}|^2 &= 1 \\ |S_{12}|^2 + |S_{24}|^2 &= 1 \\ |S_{13}|^2 + |S_{34}|^2 &= 1 \\ |S_{24}|^2 + |S_{34}|^2 &= 1 \end{aligned} \end{gather} $$

2. 进一步得到, 并设置Reference Plane进行假设

$$ \begin{gather} \begin{aligned} |S_{12}| &= |S_{34}| \\ |S_{13}| &= |S_{24}| \\ S_{12} &= S_{34} = \alpha \\ S_{13} &= \beta e^{j \theta}, S_{24} = \beta e^{j \phi} \end{aligned} \end{gather} $$

3. 继续利用Unitary Matrix的性质

• Multilication of Row 2 & 3

$$ \begin{gather} \begin{aligned} S_{12}’ S_{13} + S_{24}’ S_{34} &= 0 \\ \tan( \theta) + \tan( \phi) &= 0 \\ \therefore \theta + \phi &= \pi \pm 2n \pi \\ \alpha^2 + \beta^2 &= 1 \end{aligned} \end{gather} $$

4. 通常$\theta$和$\phi$有两种取值

• $\theta = \phi = \dfrac{ \pi }{ 2 }$, Symmetrical Coupler

$$ \begin{gather} \begin{aligned} [S] &= \begin{bmatrix} 0 & \alpha & j \beta & 0 \\ \alpha & 0 & 0 & j \beta \\ j \beta & 0 & 0 & \alpha \\ 0 & j \beta & \alpha & 0 \end{bmatrix} \end{aligned} \end{gather} $$

• $\theta = 0, \phi = \pi$, AntiSymmetrical Coupler

$$ \begin{gather} \begin{aligned} [S] &= \begin{bmatrix} 0 & \alpha & \beta & 0 \\ \alpha & 0 & 0 & -\beta \\ \beta & 0 & 0 & \alpha \\ 0 & - \beta & \alpha & 0 \end{bmatrix} \end{aligned} \end{gather} $$

Solution II

• $S_{13} = S_{24}, S_{12} = S_{34}$

• 最终得到$[S] = 0$. 这样一个设备是没有意义的

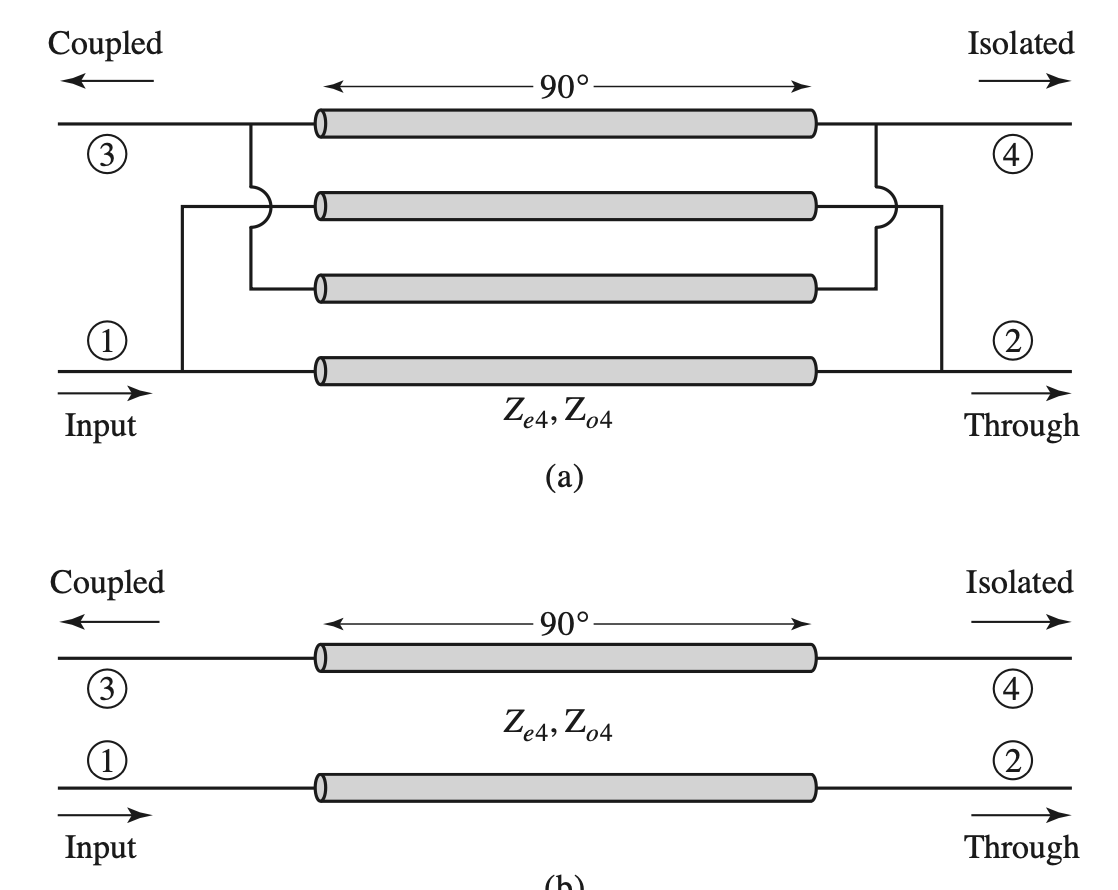
Directional Coupler

$$ \begin{gather} \begin{aligned} C &= 10 \cdot log( \frac{ P_1 }{ P_3 }) = -20 \cdot log \beta (dB) \\ D &= 10 \cdot log( \frac{ P_3 }{ P_4 }) = 20 \cdot log ( \frac{ \alpha }{ |S_{14}|}) (dB) \\ I &= 10 \cdot log( \frac{ P_1 }{ P_4 }) = - 20 \cdot log( |S_{14}|) (dB) \\ IL &= 10 \cdot log( \frac{ P_1 }{ P_2 }) = -20 log( |S_{12}|)(dB) \\ I &= (C+D) ( dB) \end{aligned} \end{gather} $$

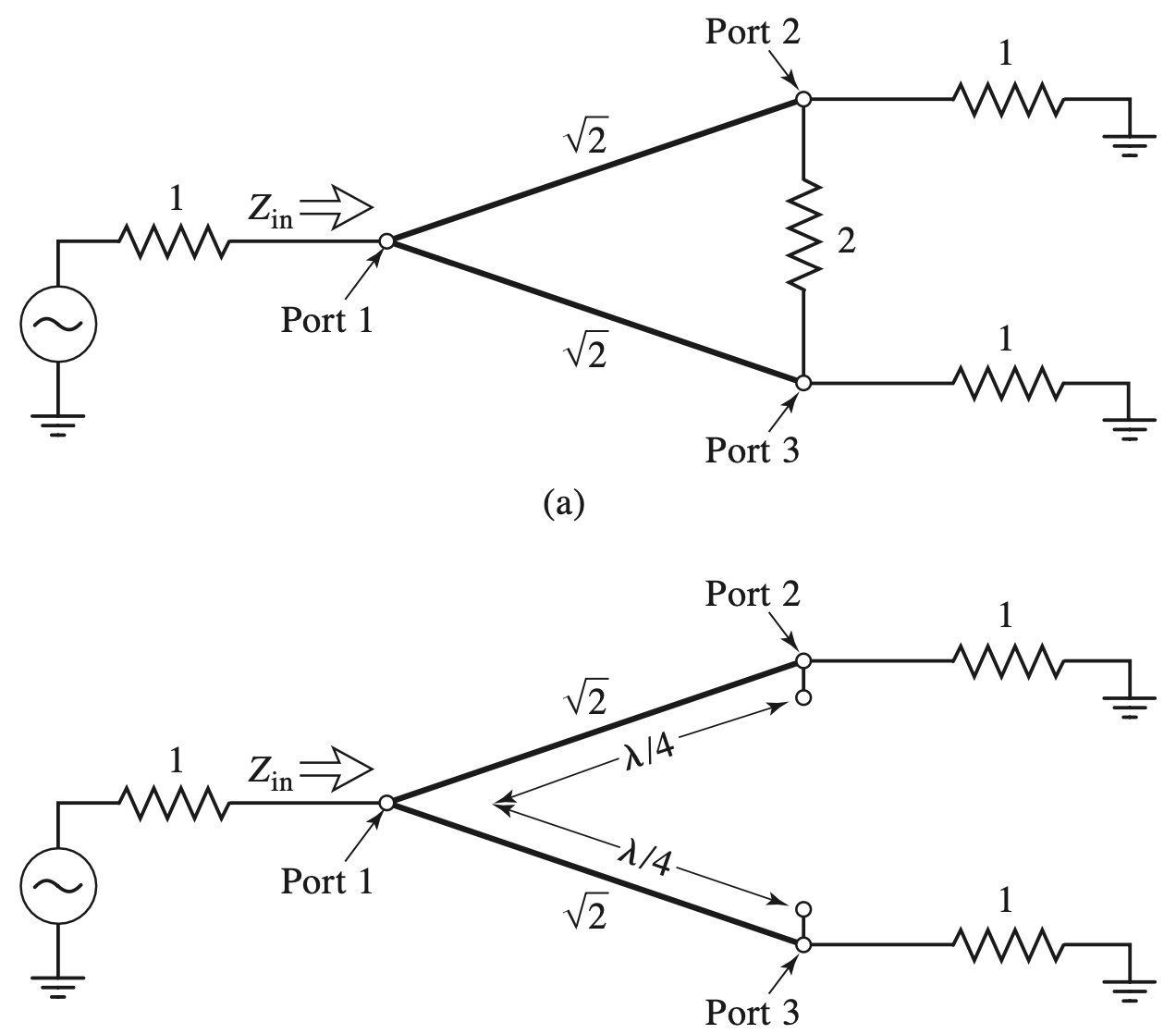
T-Junciton Power Divider

Lossless Divider

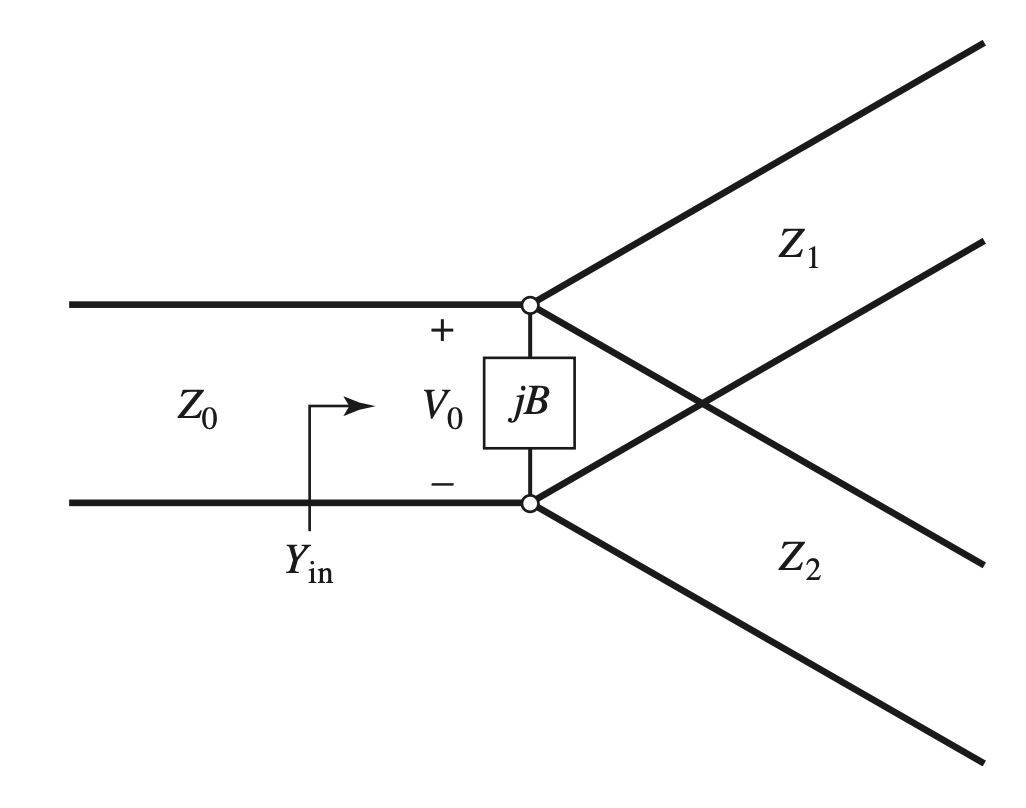
$$ \begin{gather} \begin{aligned} Y_{in} &= \frac{ 1 }{ Z_0 } \\ &= \frac{ 1 }{ Z_1 } + \frac{ 1 }{ Z_2 } + jB \end{aligned} \end{gather} $$

Resistive Divider

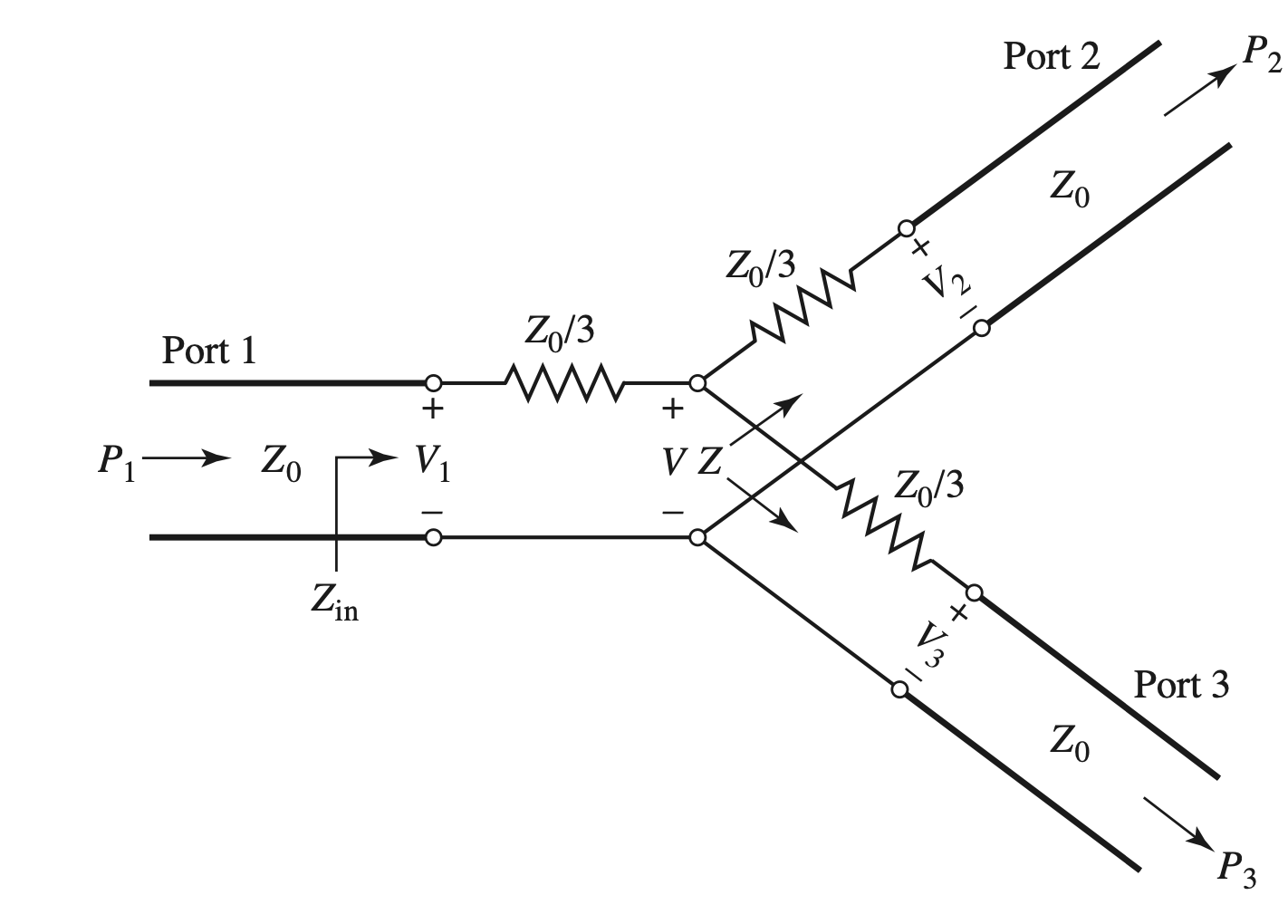
1. 电路分析

$$ \begin{gather} \begin{aligned} Z &= \frac{ Z_0 }{ 3 } + Z_0 = \frac{ 4 }{ 3 } Z_0 \\ Z_{in} &= \frac{ Z_0 }{ 3 } + \frac{ 4 }{ 3 } Z_0 || \frac{ 4 }{ 3 } Z_0 = Z_0 \\ \therefore V &= \frac{ 2 }{ 3 }V_1 \\ V_2 &= V_3 = \frac{ 1 }{ 2 } V_1 \\ \therefore S_{12} &= S_{13} = S_{23} = \frac{ 1 }{ 2 } \end{aligned} \end{gather} $$

2. 阻抗匹配时的S参数

$$ \begin{gather} \begin{aligned} [S] &= \frac{ 1 }{ 2 } \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{bmatrix} \\ [S]^t [S]’ &\neq [U] \end{aligned} \end{gather} $$

• 不是Unitary Matrix

3. Power

$$ \begin{gather} \begin{aligned} P_{in} &= \frac{ V_1^2 }{ 2 Z_0 } \\ P_2 = P_3 &= \frac{ (\dfrac{ 1 }{ 2 } V_1)^2 }{ 2Z_0 } = \frac{ 1 }{ 4 } P_{in} \\ P_{loss} &= \frac{ 1 }{ 2 } P_{in} \end{aligned} \end{gather} $$

• 可以看出，损失了一半的能量

Wilkinson Power Divider

Circuits

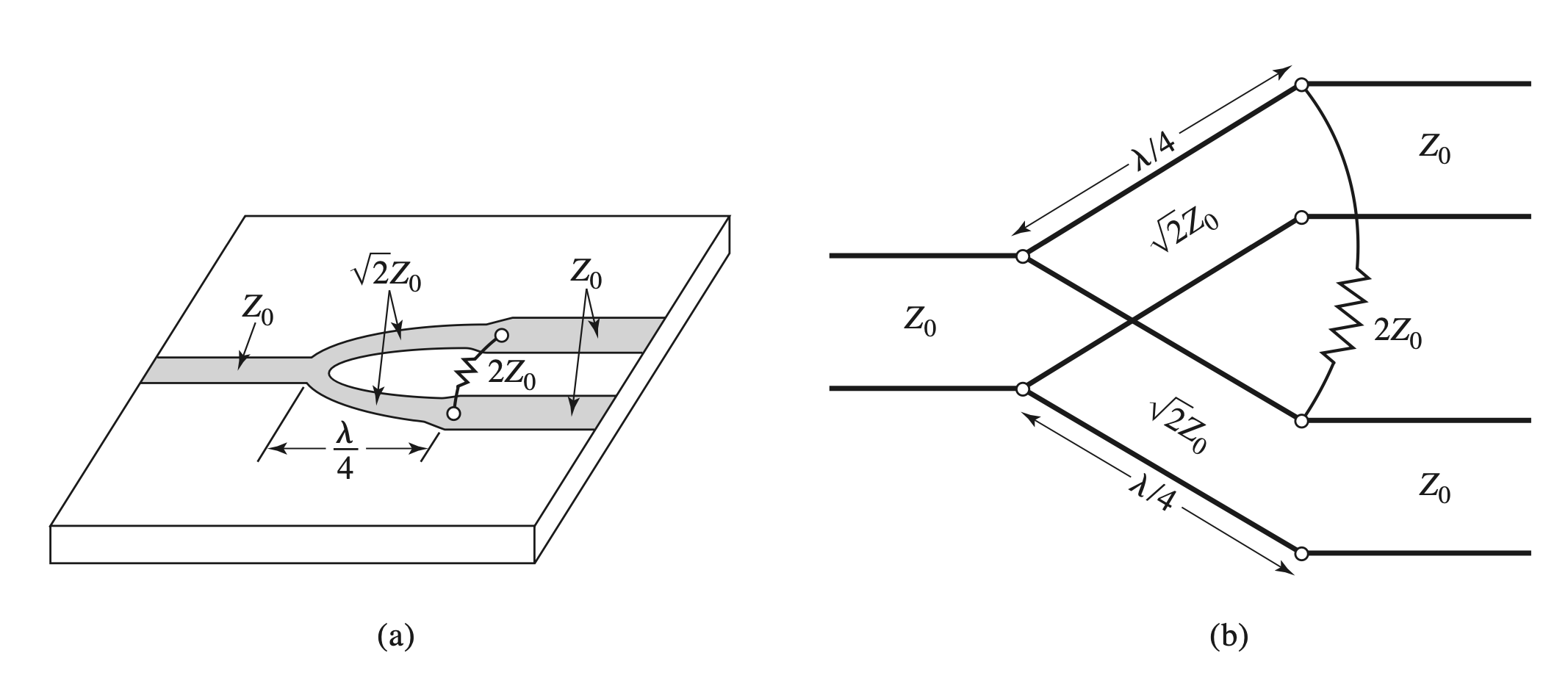
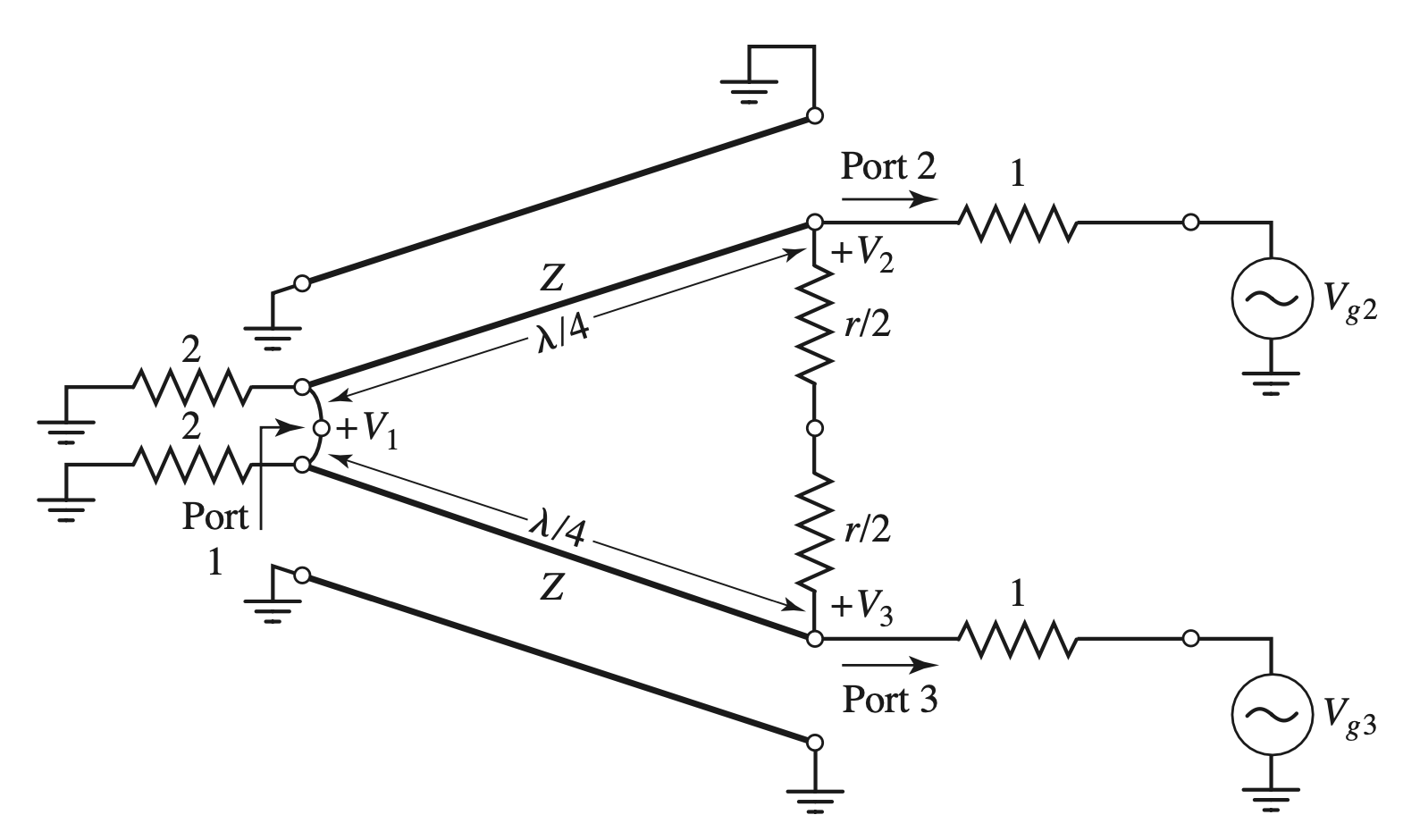
Analysis

Even Mode Analysis

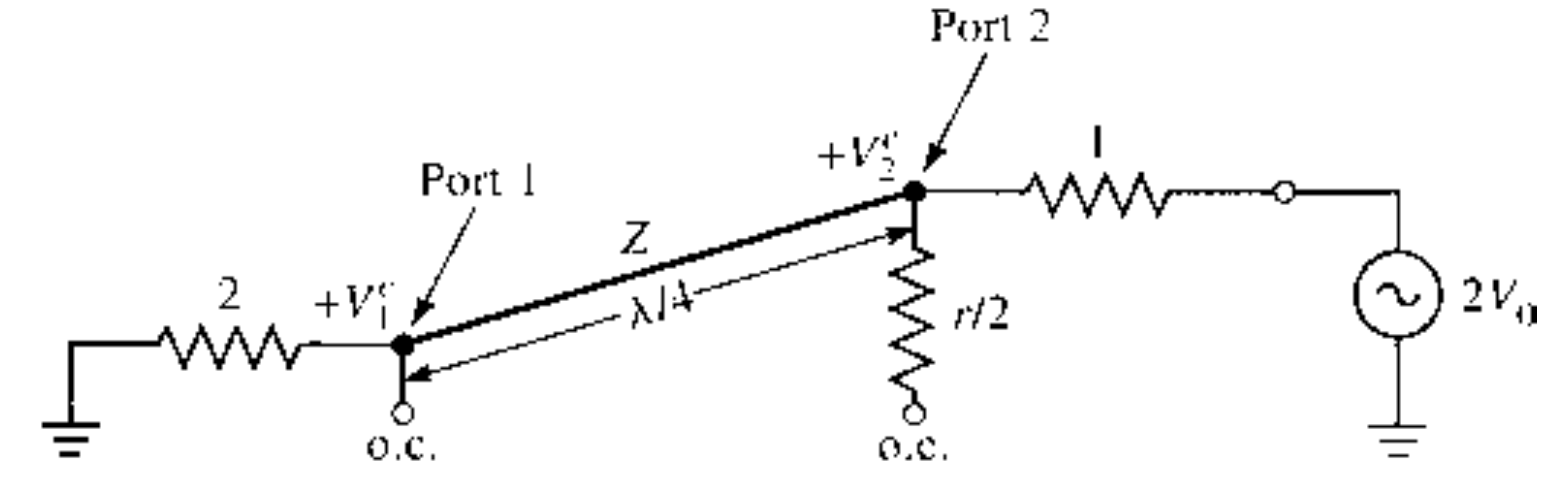
1. $V_2^e$

• $Z = \sqrt{ 2 }$

$$ \begin{gather} \begin{aligned} V_{g1} &= V_{g2} = 2V_0 \\ Z_{in}^e &= \frac{ Z_0^2 }{ Z_L } = \frac{ Z^2 }{ 2 } = 1 \\ \therefore V_2^e &= V_0 \end{aligned} \end{gather} $$

2. $V_1^e$

$$ \begin{gather} \begin{aligned} V(x) &= V^+(e^{-j \beta x} + \Gamma e^{j \beta x}) \\ V_2^e &= V(- \frac{ \lambda }{ 4 }) = j V^+ ( 1- \Gamma) = V_0 \\ V_1^e &= V(0) = V^+ ( 1 + \Gamma) = j V_0 \frac{ \Gamma + 1 }{ \Gamma -1 } \\ \Gamma &= \frac{ Z_{in 1} - Z_0}{ Z_{in1} + Z_0 } \\ &= \frac{ 2 - \sqrt{ 2 } }{ 2 + \sqrt{ 2 } } \\ \therefore V_1^e &= -j V_0 \sqrt{ 2 } \end{aligned} \end{gather} $$

Odd Mode Analysis

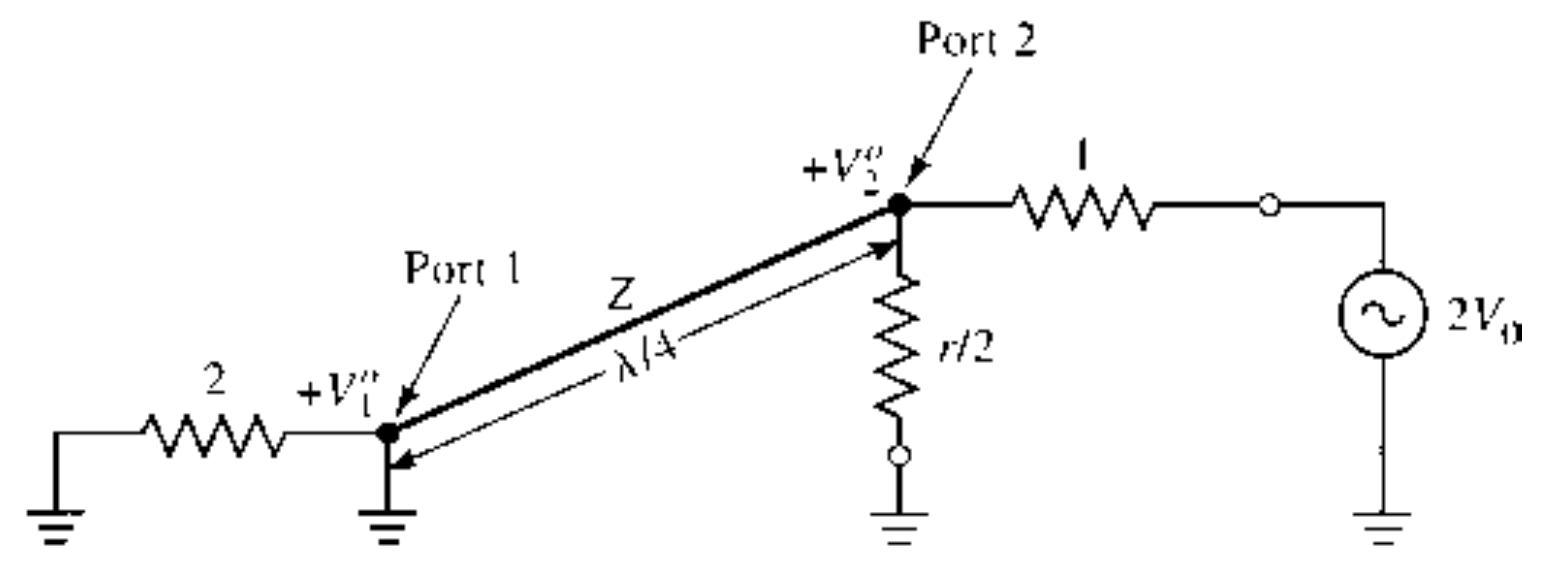
1. Voltage Analysis

• $r = 2$

$$ \begin{gather} \begin{aligned} V_{g2} &= -V_{g3} = 2V_0 \\ V_2^o &= - V_3^o \\ Z_{in2} &= \infin || \frac{ r }{ 2 } = \frac{ r }{ 2 } = 1 \\ \therefore V_2^o &= V_0 \\ V_1^o &= 0 \end{aligned} \end{gather} $$

2. $Z_{in1}$

$$ \begin{gather} \begin{aligned} Z_{in1} &= \frac{ Z_0^2 }{ Z_L } = 1 \end{aligned} \end{gather} $$

S Params

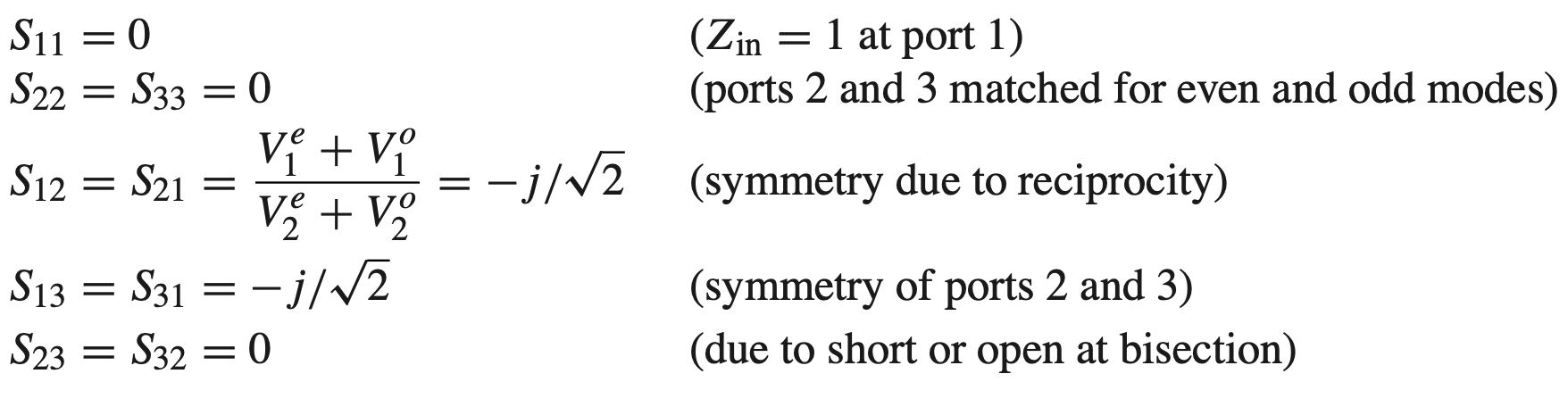
$$ \begin{gather} \begin{aligned} [S] &= -j \frac{ 1 }{ \sqrt{ 2 } } \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix} \end{aligned} \end{gather} $$

Unequal Power Devision & N-Way Wilkinson Power Divider

• $R_2, R_3$是2、3端口的匹配阻抗

$$ \begin{gather} \begin{aligned} Z_{03} &= Z_0 \sqrt{ \frac{ 1 + K }{ K^3 } } \\ Z_{02} &= K^2 Z_{03} = Z_0 \sqrt{ K(1 + K^2) } \\ R &= Z_0 ( K + \frac{ 1 }{ K }) \\ R_2 &= Z_0 K \\ R_3 &= Z_0 / K \end{aligned} \end{gather} $$

Quadarture Hybrid

Branch-Line Coupler

Circuits & S Params

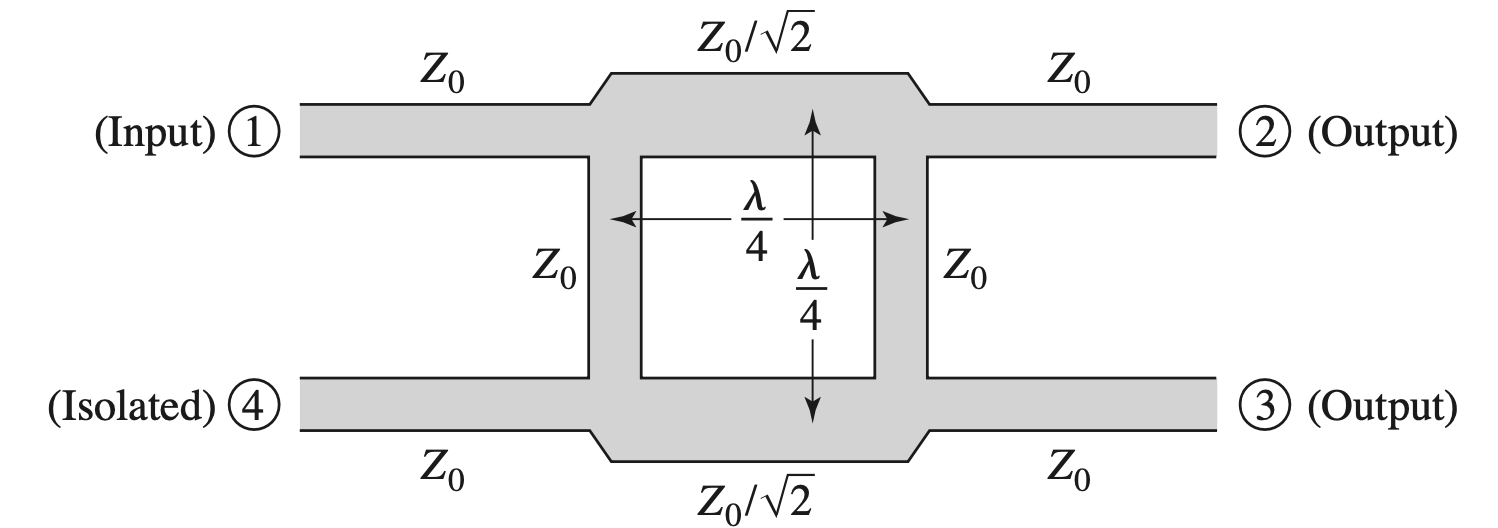
$$ \begin{gather} \begin{aligned} [S] &= - \frac{ 1 }{ \sqrt{ 2 } } \begin{bmatrix} 0 & j & 1 & 0 \\ j & 0 & 0 & 1 \\ 1 & 0 & 0 & j \\ 0 & 1 & j & 0 \end{bmatrix} \end{aligned} \end{gather} $$

Normalized Circuits

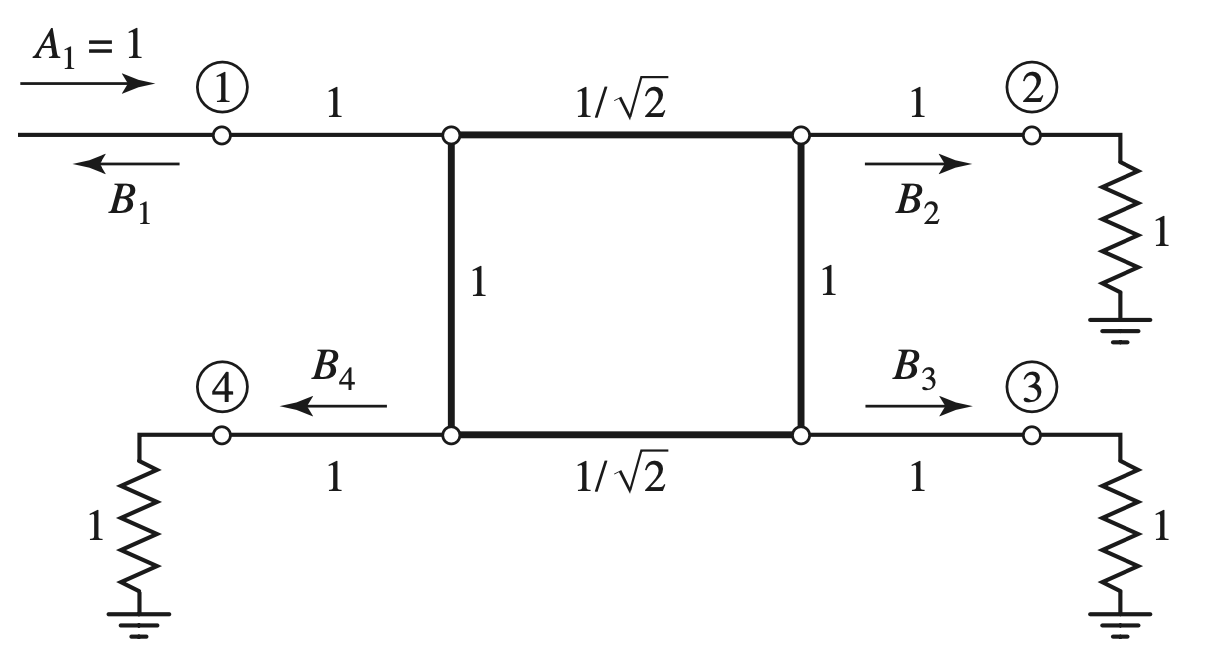
• Emerging Waves

$$ \begin{gather} \begin{aligned} B_1 &= \frac{ 1 }{ 2 } ( \Gamma_e + \Gamma_o) \\ B_2 &= \frac{ 1 }{ 2 } (T_e + T_o) \\ B_3 &= \frac{ 1 }{ 2 } ( \Gamma_e - \Gamma_o) \\ B_4 &= \frac{ 1 }{ 2 } (T_e - T_o) \end{aligned} \end{gather} $$

Even-Odd Mode Analysis

Even Mode

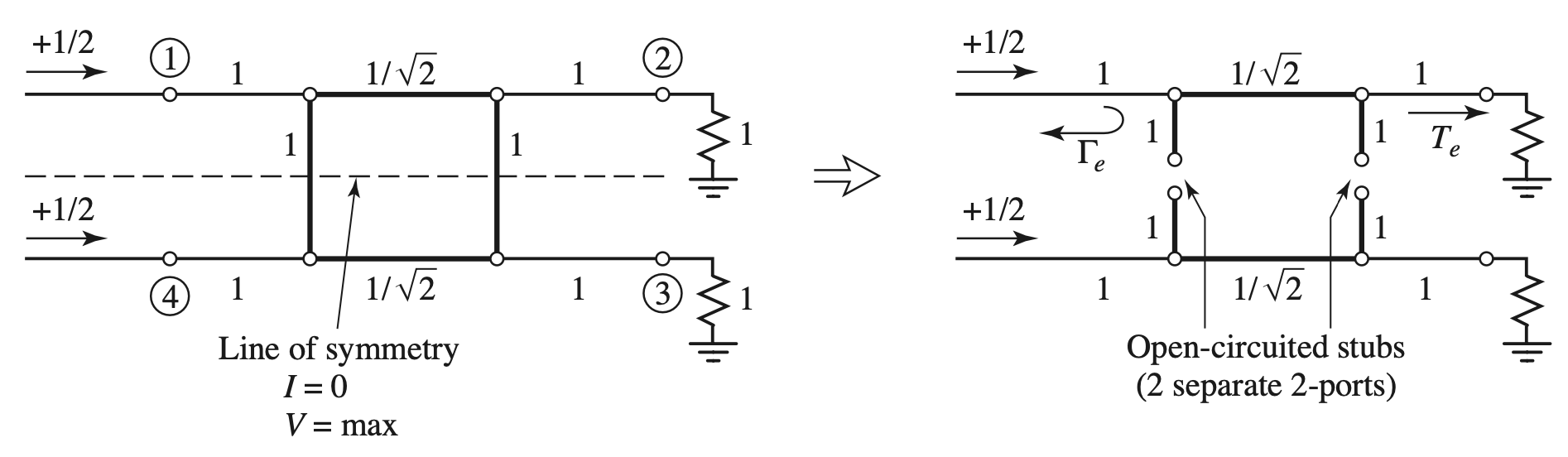
1. 该电路是Shunt Y, $\dfrac{ \lambda }{ 4 }$, Shunt Y Cascade 形成的

$$ \begin{gather} \begin{aligned} \begin{bmatrix} A & B \\ C & D \end{bmatrix}_e &= \frac{ 1 }{ \sqrt{ 2 } } \begin{bmatrix} -1 & j \\ j & -1 \end{bmatrix} \end{aligned} \end{gather} $$

2. 根据ABCD - S参数转化表

$$ \begin{gather} \begin{aligned} \Gamma_e &= S_{11}^e = 0 \\ T_e &= S_{21}^e = - \frac{ 1 }{ \sqrt{ 2 } } (1 + j) \end{aligned} \end{gather} $$

Odd Mode

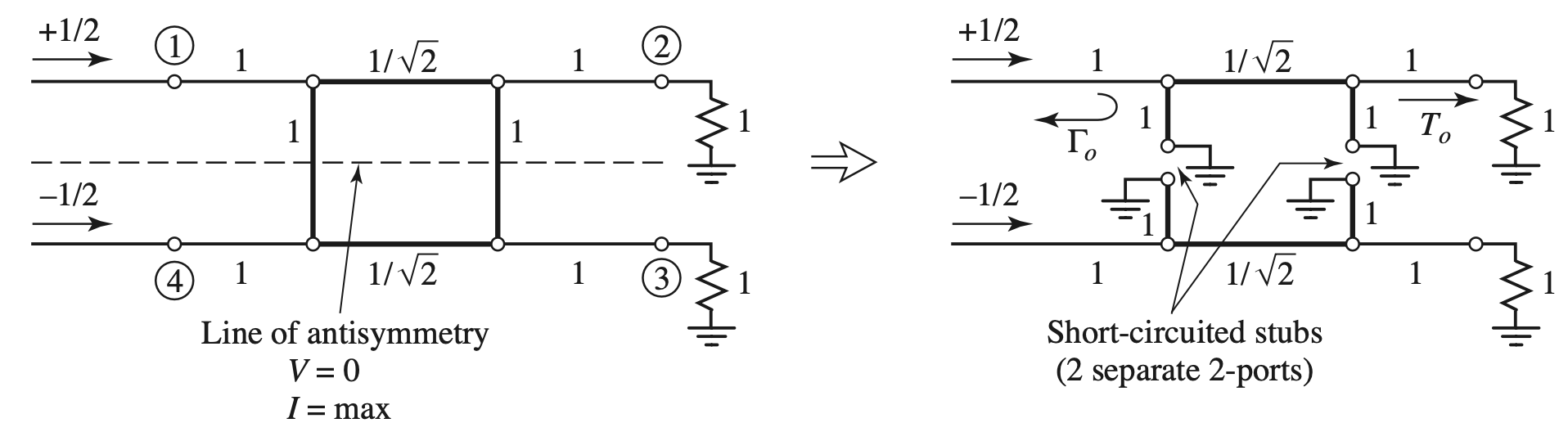
• 同理

$$ \begin{gather} \begin{aligned} \begin{bmatrix} A & B \\ C & D \end{bmatrix}_o &= \frac{ 1 }{ \sqrt{ 2 } } \begin{bmatrix} 1 & j \\ j & 1 \end{bmatrix} \\ \Gamma_o &= 0 \\ T_o &= \frac{ 1 }{ \sqrt{ 2 } } ( 1- j) \end{aligned} \end{gather} $$

Emerging Wave

$$ \begin{gather} \begin{aligned} B_1 &= 0 \\ B_2 &= - \frac{ j }{ \sqrt{ 2 } } \\ B_3 &= - \frac{ 1 }{ \sqrt{ 2 } } \\ B_4 &= 0 \end{aligned} \end{gather} $$

Coupled-Line Directional Coupler

Even-Odd Mode Analysis

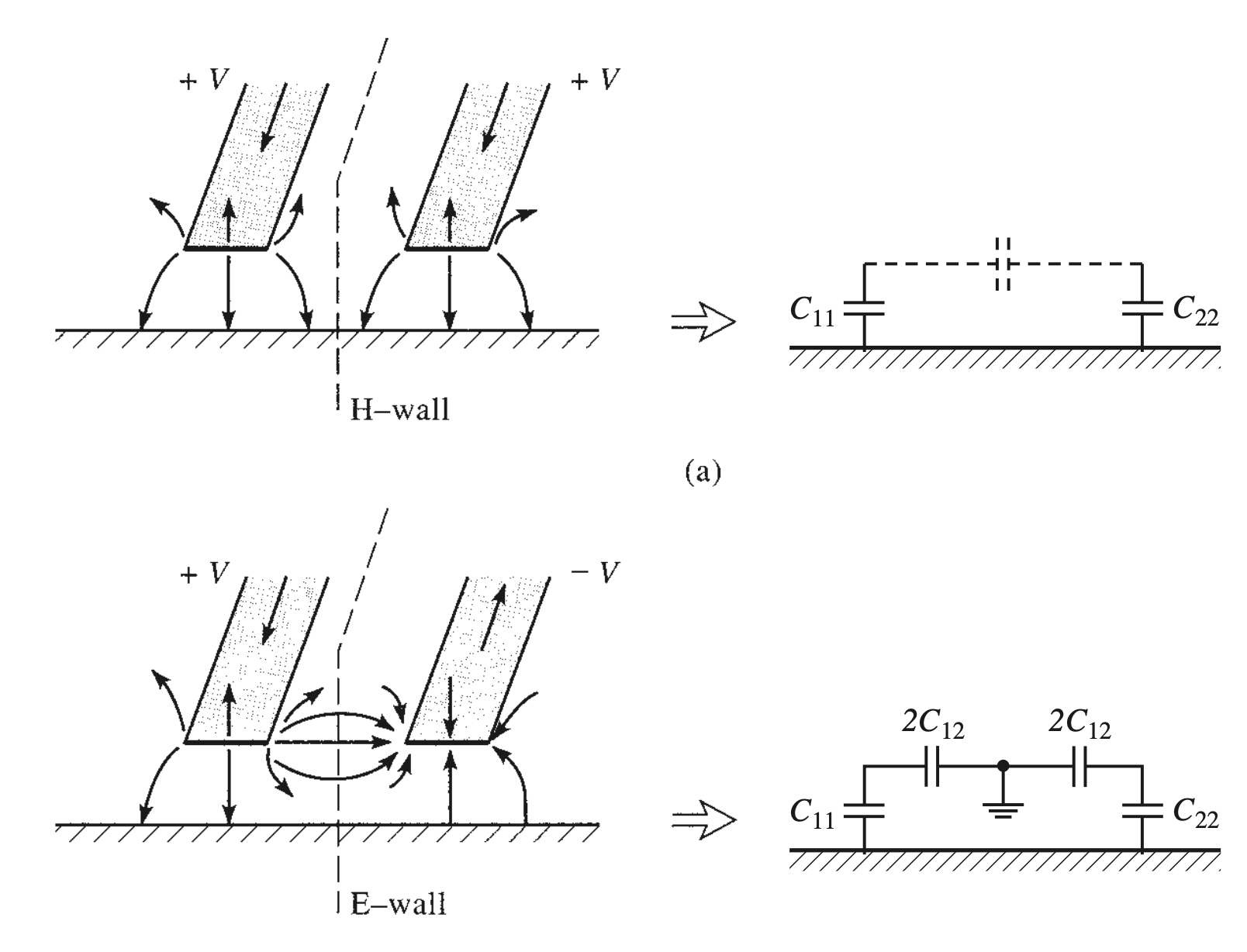
1. Even Mode

$$ \begin{gather} \begin{aligned} C_e &= C_{11} = C_{22} \\ v_p &= \frac{ 1 }{ \sqrt{ L_o C_o } } = \frac{ 1 }{ \sqrt{ L_e C_e } } \\ Z_{0e} &= \sqrt{ \frac{ L_e }{ C_e } } = \frac{ 1 }{ v_p C_e } \end{aligned} \end{gather} $$

2. Odd Mode

$$ \begin{gather} \begin{aligned} C_o &= C_{11} + 2 C_{12} \\ Z_{0o} &= \sqrt{ \frac{ L_o }{ C_o } } = \frac{ 1 }{ v_p C_o } \end{aligned} \end{gather} $$

Design of Coupled Line Couplers

Single-Section Coupled Line Coupler

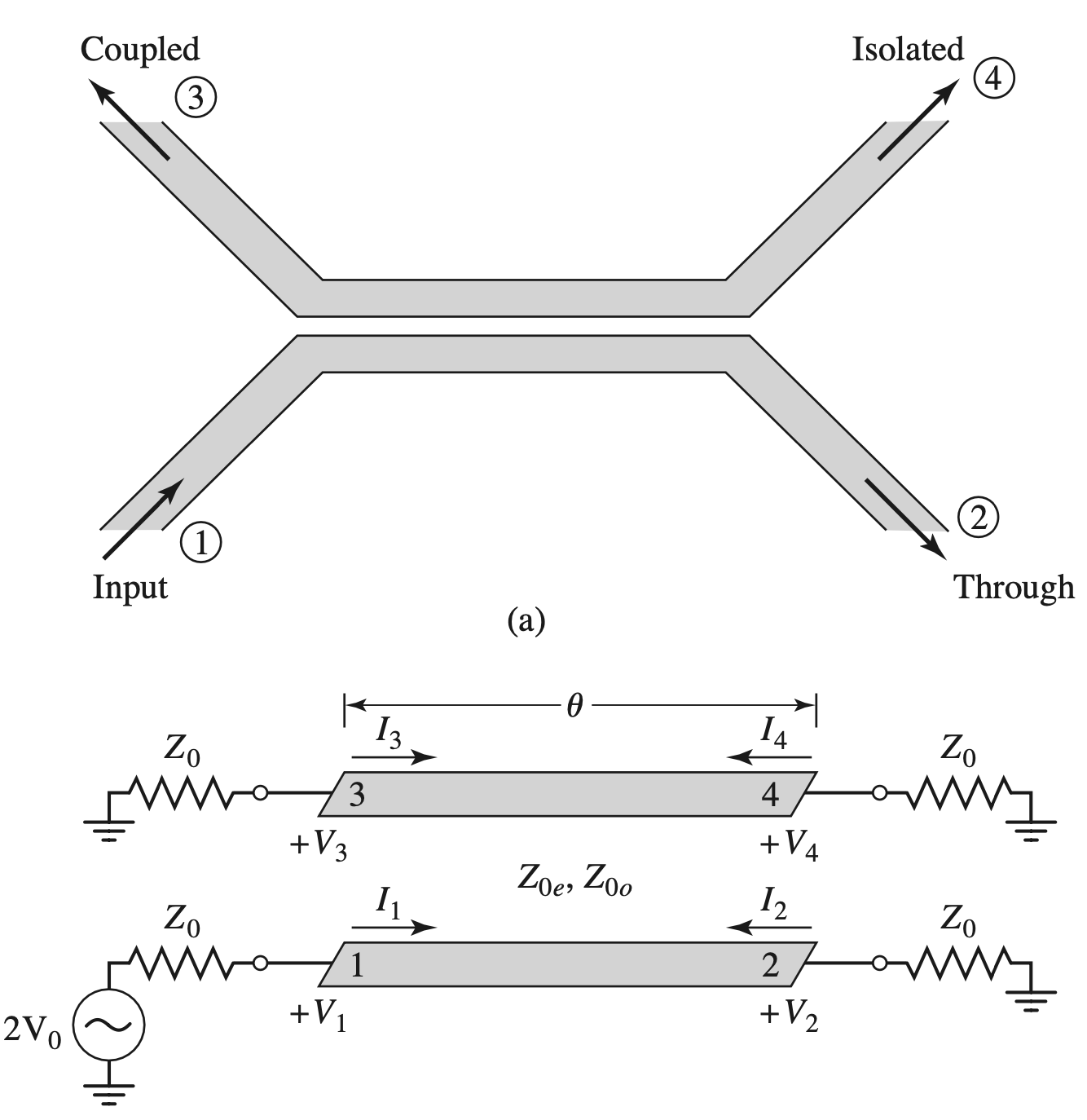
Even-Odd Mode Analysis

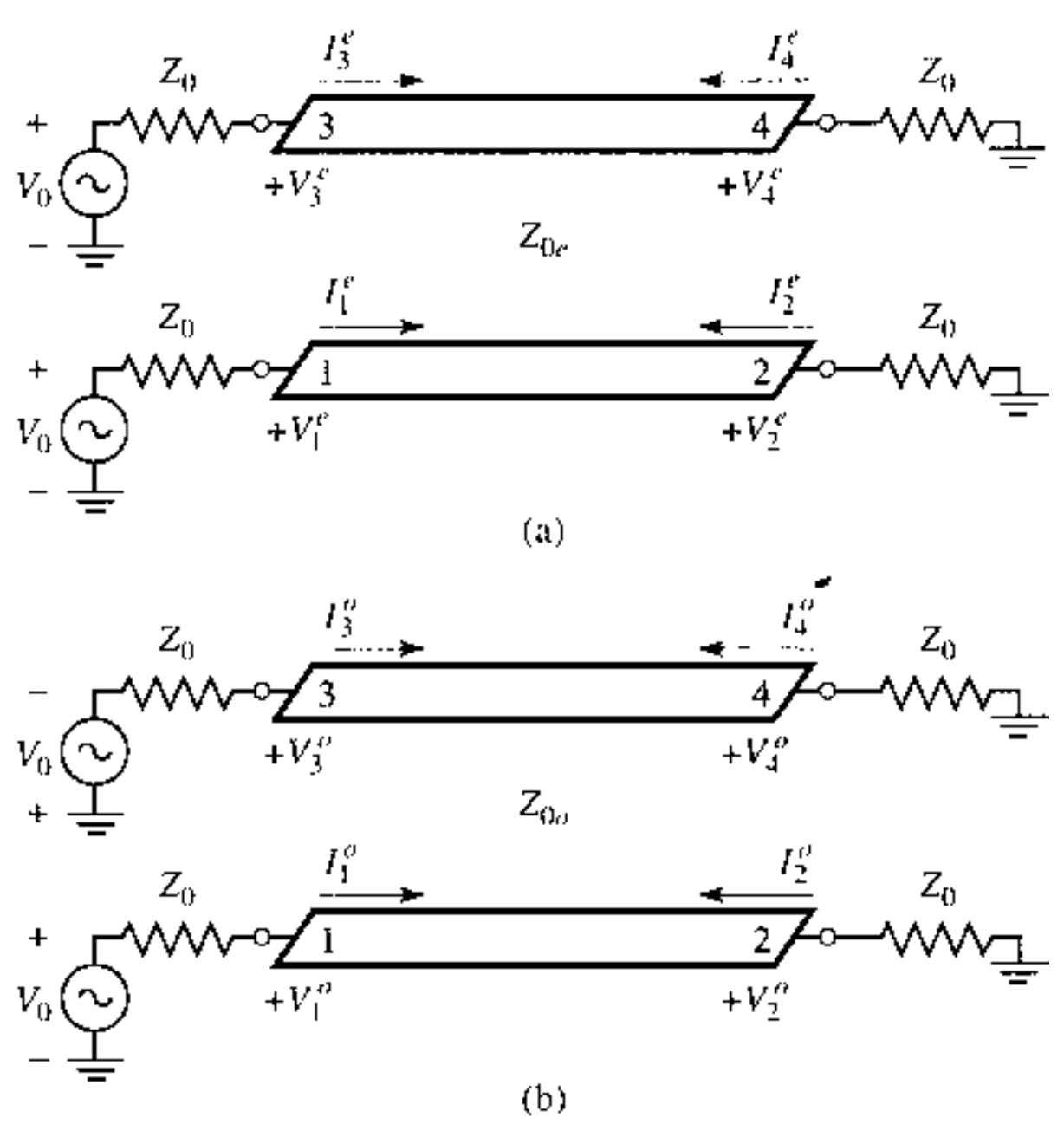
1. 回顾 Impedance Function

$$ \begin{gather} \begin{aligned} Z_{in} &= \frac{ V_1 }{ I_1 } = \frac{ V_1^e + V_1^o }{ I_1^e + I_1^o } \\ &= Z_0 \frac{ Z_0 + j Z_L \tan \theta }{ Z_L + j Z_0 \tan \theta } \end{aligned} \end{gather} $$

$$ \begin{gather} \begin{aligned} V_1^e &= V_0 \frac{ Z_{in}^e }{ Z_{in}^e + Z_0 } \\ V_1^o &= V_0 \frac{ Z_{in}^o }{ Z_{in}^o + Z_0 } \\ I_1^e &= \frac{ V_0 }{ Z_{in}^e + Z_0 } \\ I_1^o &= \frac{ V_0 }{ Z_{in}^o + Z_0 } \end{aligned} \end{gather} $$

2. 假设$Z_0 = \sqrt{ Z_{0o} Z_{0e} }$

• 可以得到

$$ \begin{gather} \begin{aligned} Z_{in} &= Z_0 \\ V_1 &= V_0 \\ V_3 &= V_3^e + V_3^o = V_1^e - V_1^o \\ &= V_0 \frac{ j (Z_{0e} - Z_{0o}) \tan \theta }{ 2 Z_0 + j (Z_{0e} + Z_{0o}) \tan \theta } \end{aligned} \end{gather} $$

3. 定义Coupling Coefficient

$$ \begin{gather} \begin{aligned} C &= \frac{ Z_{0e} - Z_{0o} }{ Z_{0e} + Z_{0o} } \\ \sqrt{ 1 - C^2 } &= \frac{ 2Z_0 }{ Z_{0e} + Z_{0o} } \end{aligned} \end{gather} $$

4. 用$C$表示各端口电压(还需要推导！！！！！)

$$ \begin{gather} \begin{aligned} V_2 &= V_2^e + V_2^o = V_0 \frac{ \sqrt{ 1 - C^2 } }{ \sqrt{ 1 - C^2 } \cos \theta + j \sin \theta} \\ V_3 &= V_0 \frac{ j C \tan \theta }{ \sqrt{ 1 - C^2 } + j \tan \theta} \\ V_4 &= V_2^e - V_2^o = 0 \end{aligned} \end{gather} $$

• 特别地，当$\theta = \dfrac{ \pi }{ 2 }$时，$\dfrac{ V_3 }{ V_1 } = C$, 此时的$C = C_0$

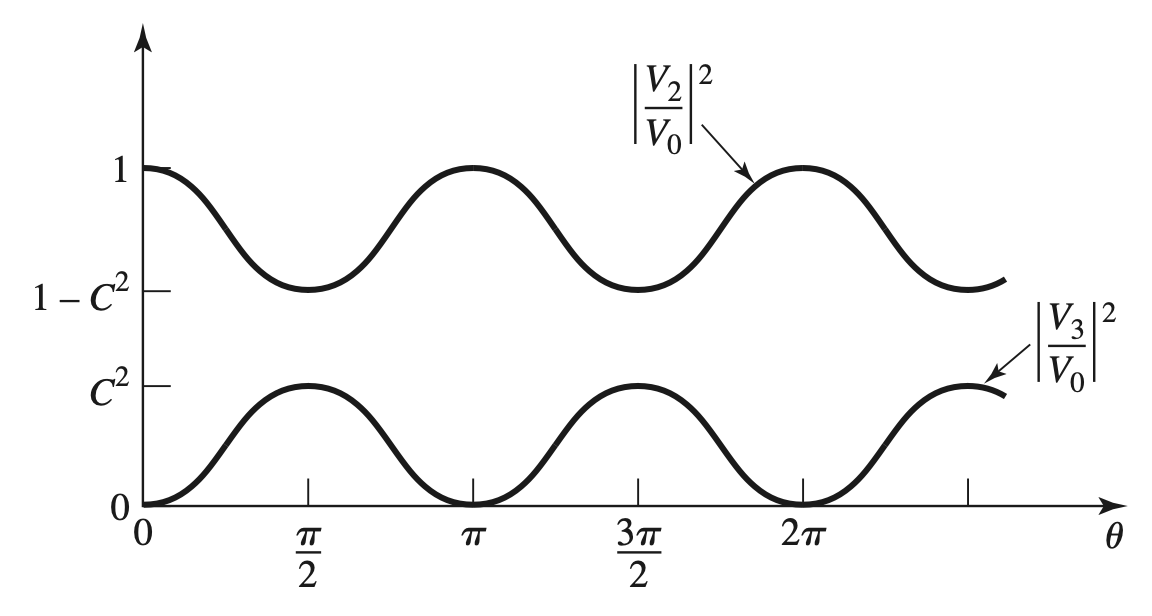
5. 用$C$表示Characteristic Impedance

$$ \begin{gather} \begin{aligned} Z_{0e} &= Z_0 \sqrt{ \frac{ 1 + C }{ 1 - C } } \\ Z_{0o} &= Z_0 \sqrt{ \frac{ 1 - C }{ 1 + C } } \end{aligned} \end{gather} $$

Design of MultiSection Coupled Line Coupler

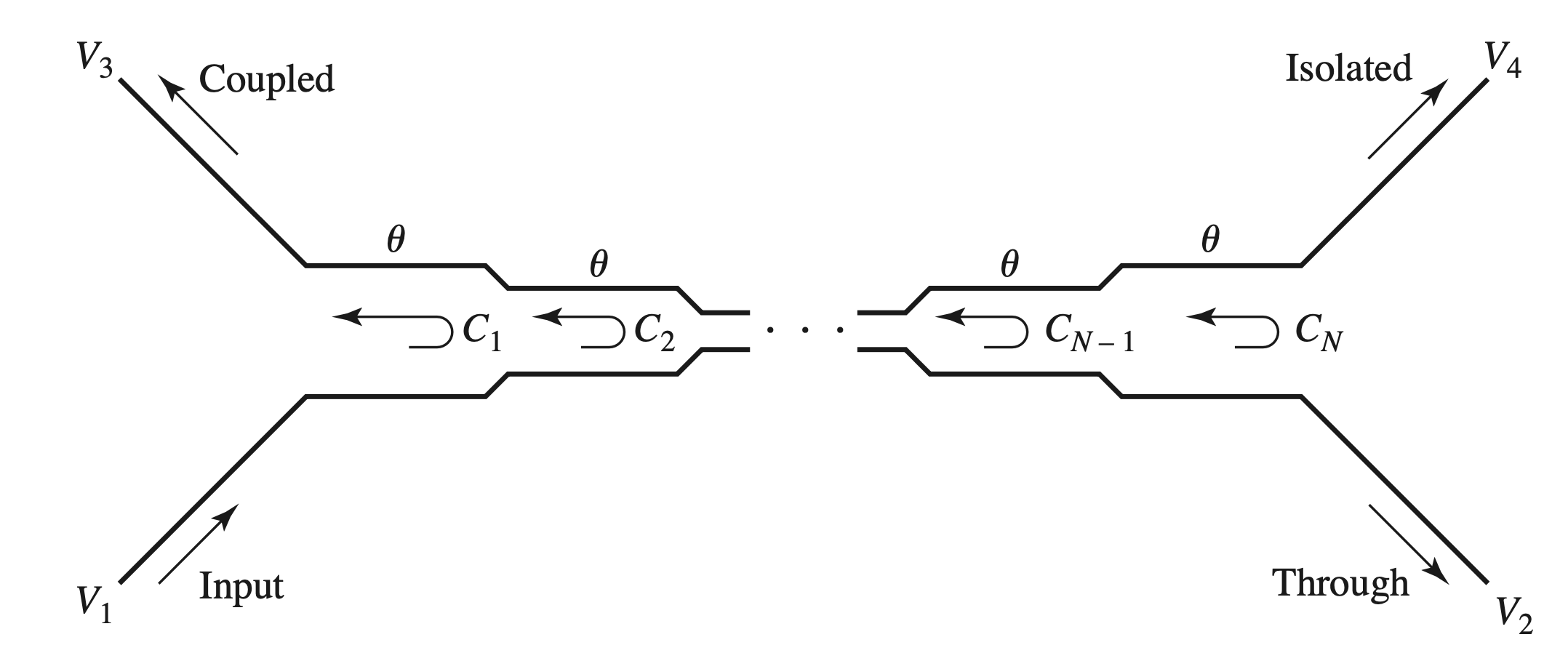
1. 假设$C \ll 1$

$$ \begin{gather} \begin{aligned} \frac{ V_2 }{ V_1 } &\approx e^{-j \theta} \\ \frac{ V_3 }{V_1 } &\approx j C \sin \theta e^{-j \theta} \end{aligned} \end{gather} $$

2. 在多段耦合线中

• 考虑到两段完全对称

$$ \begin{gather} \begin{aligned} V_3 &= jV_1 \sin \theta e^{-j \theta} \Big[ C_1 +C_2 e^{-2j \theta} + … + C_N e^{-2j (N-1) \theta} \Big] \\ &= jV_1 \sin \theta e^{-j \theta} \Big[ C_1(1 + e^{-2j (N-1) \theta}) + C_2(e^{-2j \theta} + e^{-2j(N-2) \theta}) + … + C_M e^{-j (N-1) \theta}\Big] \\ &= 2j V_1 \sin \theta e^{-j N \theta} \Big[ C_1 \cos(N-1) \theta + C_2 \cos(N-3) \theta + … + \frac{ 1 }{ 2 } C_M \Big]\\ M &= \frac{ N+1 }{ 2 } \end{aligned} \end{gather} $$

Lange Coupler (未完待续)

Topology & Circuit

Topology of Folded & Unfolded Lange Coupler

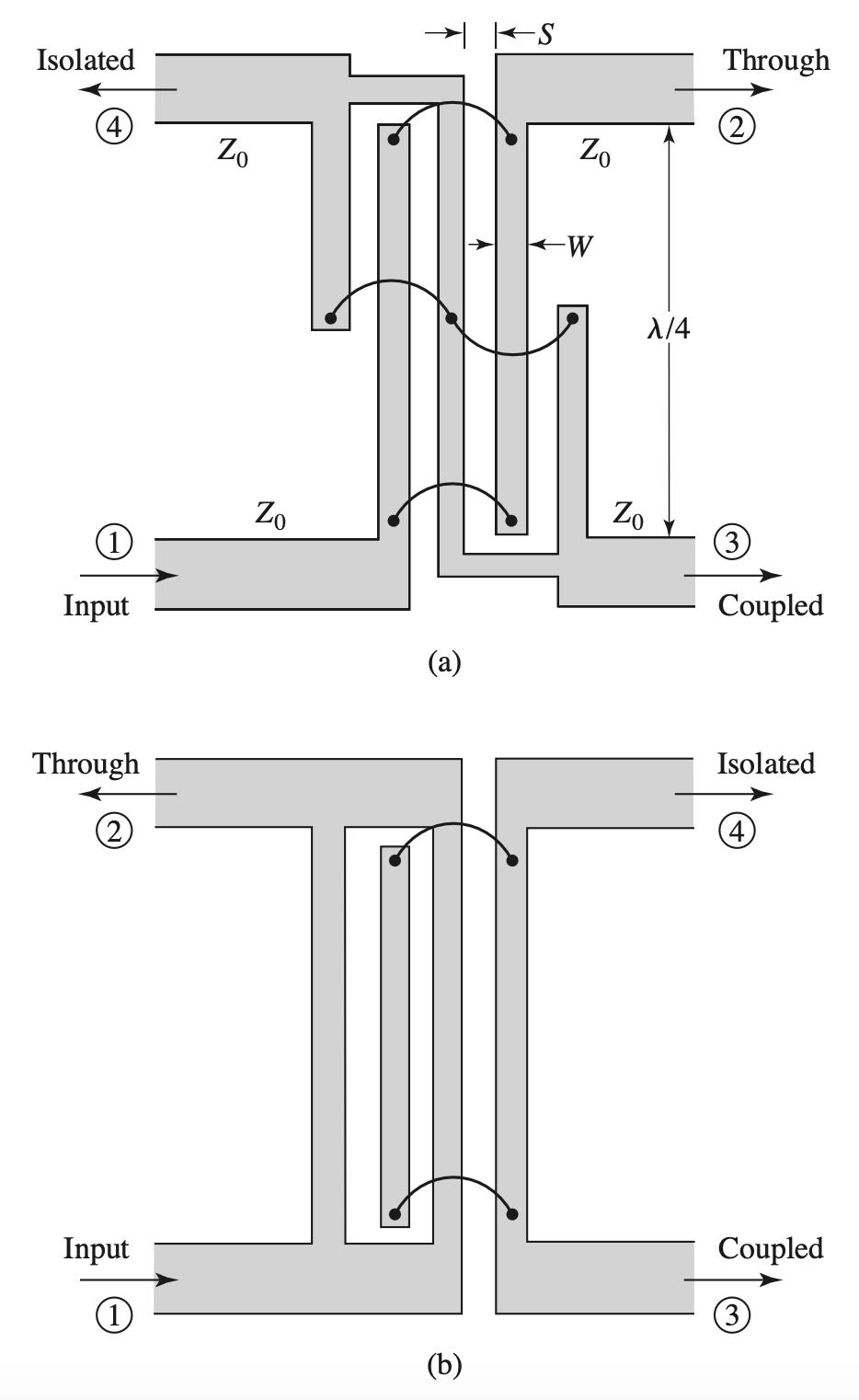
Circuit of Unfolded Lange Coupler

180 Degree Coupler