Laplace Transform

Definition

$$ \begin{gather} \begin{aligned} X(s) &= \int_{ - \infin }^{ \infin } x(t) e^{- s t} dt \\ s &= \alpha + j \omega \end{aligned} \end{gather} $$

Relations with Fourier Transform

1. 当$\alpha = 0$时, $X(s)$就是$x(t)$的傅立叶变换

$$ \begin{gather} \begin{aligned} X(j \omega) &= \int_{ - \infin }^{ \infin } x(t) e^{-j \omega t} dt \end{aligned} \end{gather} $$

2. 当$\alpha \neq 0$时, $X(s)$是$x(t)$乘以实信号$e^{ \alpha t}$之后的傅立叶变换

$$ \begin{gather} \begin{aligned} X(s) &= \int_{ - \infin }^{ \infin } [x(t) e^{- \alpha t}] e^{-j \omega t} \end{aligned} \end{gather} $$

ROC (Region of Convergence)

Rational Laplace Transform

ROC是由使得$X(s)$收敛的$s$组成的

• 只要$x(t)$是复指数信号的线性组合，$X(s)$就是有理的, $N(s)$和$D(s)$也可以用它们的根来表示

$$ \begin{gather} \begin{aligned} X(s) &= \frac{ N(s) }{ D(s) } \end{aligned} \end{gather} $$

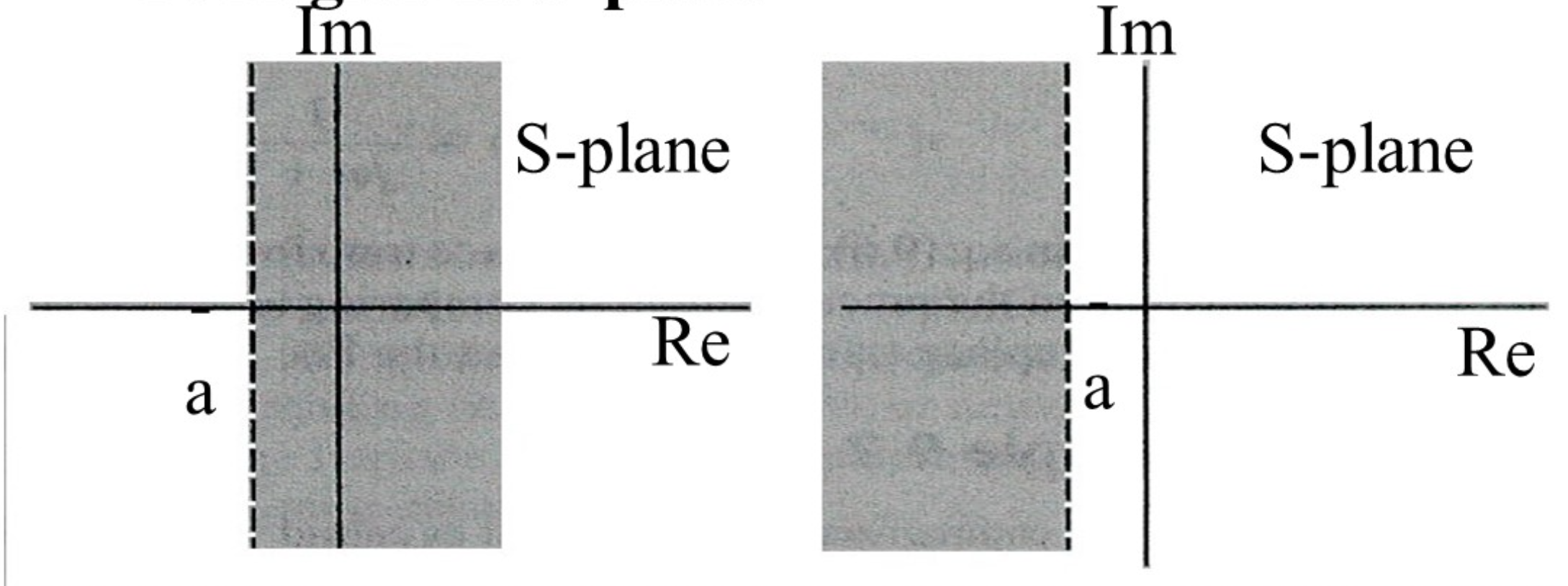
Properties

1. $X(s)$收敛的条件是

$$ \begin{gather} \begin{aligned} |\int_{ - \infin }^{ \infin } x(t) e^{- \alpha t} dt| < \infin \end{aligned} \end{gather} $$

• ROC由$\alpha$而不是$\omega$决定

2. 有理拉普拉斯变换的收敛域没有极点， 边界由极点定义(没有极点就没有边界)

Z Transform

Definition

$$ \begin{gather} \begin{aligned} X(z) &= \sum_{ n = - \infin }^{ \infin } x[n] z^{-n} \\ x[n] &\overset{ Z }{ \longleftrightarrow } X(z) \\ z &= re^{j \omega} \end{aligned} \end{gather} $$

与 FT 的关系

$$ \begin{gather} \begin{aligned} X(z) &= \mathcal{F} \Big\lbrace x[n] r^{-n}\Big\rbrace \end{aligned} \end{gather} $$

Inverse Z Transform

Definition

$$ \begin{gather} \begin{aligned} x[n] &= \frac{ 1 }{ 2 \pi j } \oint_{ }^{ } X(z) z^{n-1} dz \end{aligned} \end{gather} $$

Solving Methods

Partial Fraction

$$ \begin{gather} \begin{aligned} X(z) &= \sum_{i = 1 }^{ m } \frac{ A_i }{ 1 - a_i z^{-1} } \\ x_i[n] &= A_i a_i^n u[n] \\ or \ x_i[n] &= -A_i a_i^n u[-n-1] \end{aligned} \end{gather} $$

Power Series Expansion

1. Compared with Definition

$$ \begin{gather} \begin{aligned} X(z) &= \sum_{ i = 0 }^{ N } a_i z^i \\ x[n] &= a_i, n = -i \end{aligned} \end{gather} $$

2. Long Division

3. Tailor’s Series

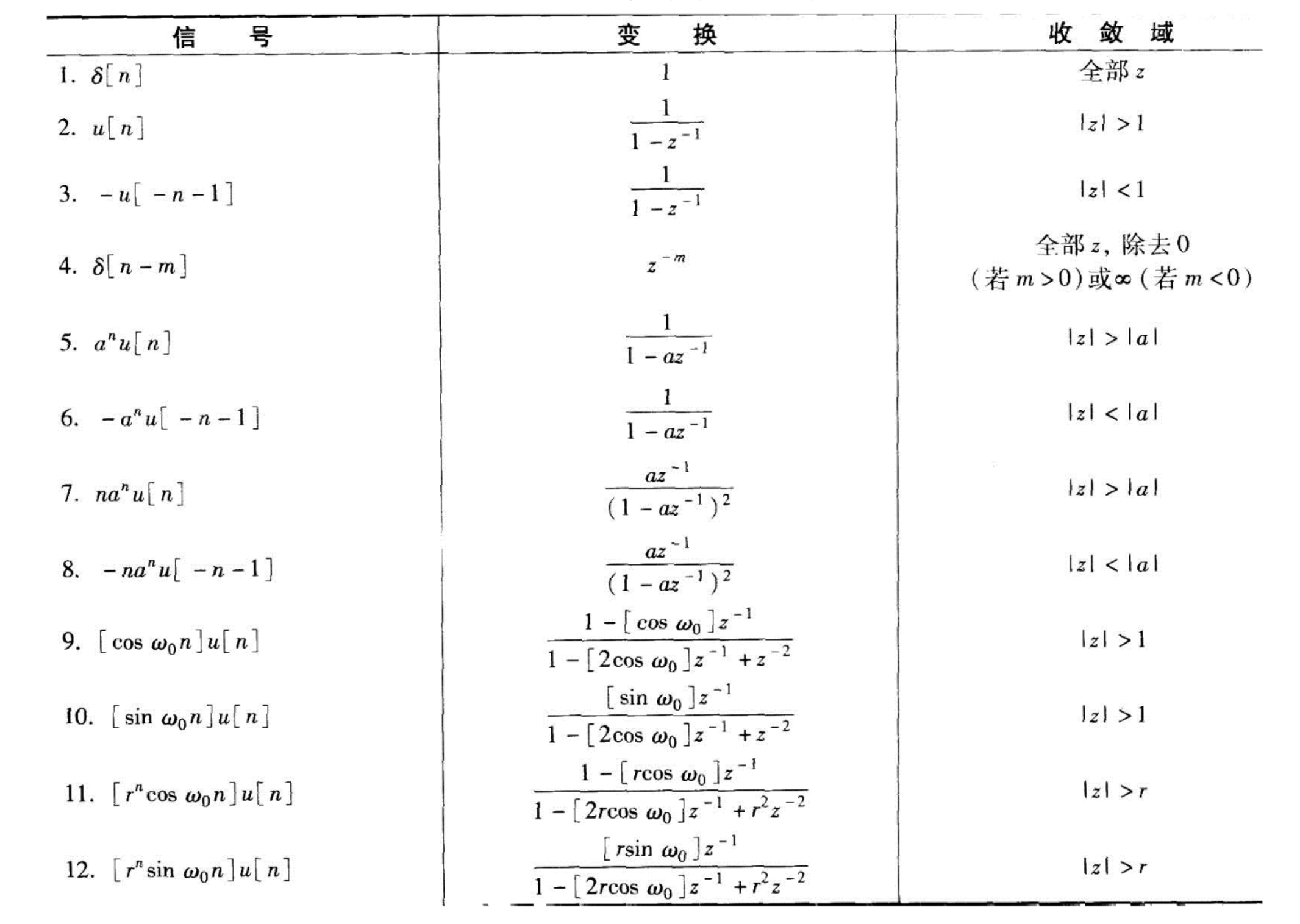
性质 & 常见Z变换对

性质

变换对

Unilateral ZT

$$ \begin{gather} \begin{aligned} X^{UZ}(z) &= \sum_{ n = 0 }^{ \infin } x[n] z^{-n} \end{aligned} \end{gather} $$

Appendix

Conjugation Formulas

$$ \begin{gather} \begin{aligned} (AB)^* &= A^B^ \\ (A^B)^ &= AB^* \end{aligned} \end{gather} $$

Finite Duration

1. $f(t)$在$[0,T]$上有值，其他区域为$0$

2. 收敛函数的收敛域必包含$j \omega$

Sigularity Function & Laplace Transform

$$ \begin{gather} \begin{aligned} u_k(t) &\overset{ \mathcal{L} }{ \longleftrightarrow } s^k \\ u_0(t) &= \delta (t) \overset{ \mathcal{L} }{ \longleftrightarrow } 1 = s^0 \\ u_{-1}(t) &= u(t) \overset{ \mathcal{L} }{ \longleftrightarrow } s^{-1} = \frac{ 1 }{ s } \end{aligned} \end{gather} $$