Machine Learning Basics

Learning Algorithms

Definition

一个计算机程序以Performace P从有关Task T的Experience E中学习

Description

Example

Feature(被量化的特征)的集合
$x\in\R^n$,每一个$x_i$都是一个feature

通过计算机处理Example的方式来定义Machine Learning

Common Tasks that can be done by Machine Learning

Classification(With Missing Inputs)
Regression(回归)

预测

Transcription

把无序的数据变成固定的、有序的形式

Translation

Performace Measure P

Accuracy

正确输出的比例

Error Rate

错误输出的比例

Experience E

Unsupervised Learning Algorithms

学习$\pmb x$并得到它的$p(\pmb x)$

Supervised Learning Algorithms

学习$\pmb{x和y}$,并最终通过$\pmb x$预测$\pmb y$

以上两个术语并不是严格定义的

Linear Regression

$$ \hat y =\pmb{w^Tx} + b\\\ \\ MSE_{test} = \frac{1}{m}\sum_i(\pmb {\hat y}{test} - \pmb y{test})^2_i = \frac{1}{m}||\pmb {\hat y}{test} - \pmb y{test}||2^2 \\\ \\ To \ minimize, \ \nabla\omega \frac{1}{m} ||\hat {\pmb y}^{(train)} - \pmb y^{(train)} ||2^2 = 0 \\\ \\ \nabla\omega \frac{1}{m} || \pmb X^{(train)}\pmb w - \pmb y^{(train)} ||_2^2 = 0 \\\ \\ \nabla_w (\pmb X^{(train)}\pmb w - \pmb y^{(train)})^T (\pmb X^{(train)}\pmb w - \pmb y^{(train)}) = 0 \\\ \\ \pmb w = (\pmb X^{(train)T}\pmb X^{(train)})^{-1} \pmb X^{(train)T}y^{(train)} $$

满足上述条件的叫做Normal Equation

Capacity, Underfitting, Overfitting

Introduction

Generalization: 预测数据的能力
Data generating distribution$p_{data}$
Training Error and Test Error

Training Error通常比Test Error低
Test Error是更重要的评估指标

Underfitting Overfitting Capacity

Underfitting Overfitting

Underfitting	Overfitting
两种误差都很高	Training Error高，Test Error低

Capacity

训练模型适应新数据的能力
以下示例对应一次，2次，9次多项式模型

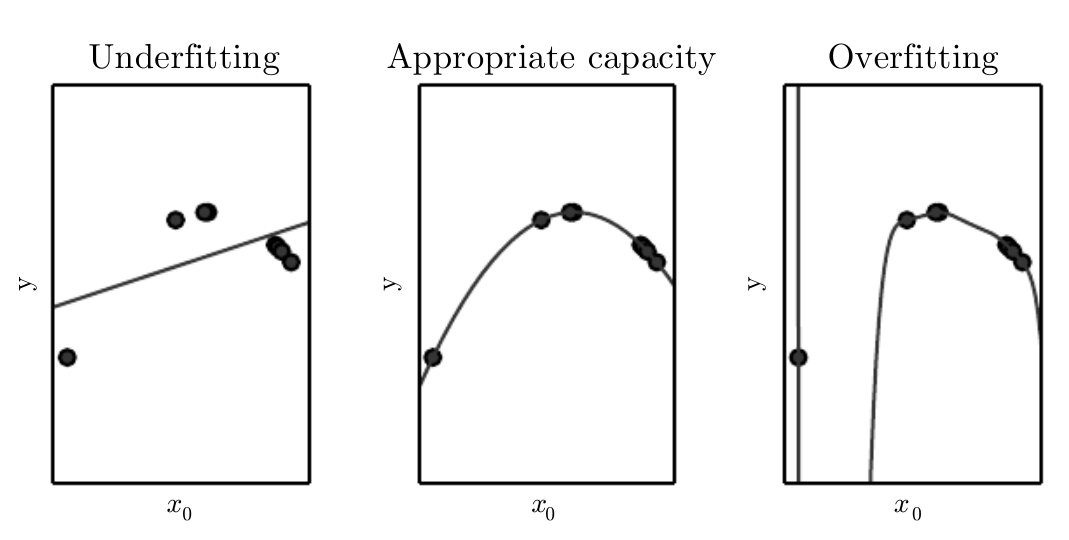
Adjust Capacity

调整参数
增加数据量大小
换训练模型

Non-parametric Model ; Bayes Error

Non-parametric Model

它在训练数据集中找到与新数据点最接近的k个数据点，然后将它们的输出值进行加权平均，作为新数据点的输出值。

$$ When \ i = min||\pmb X_i -\pmb x||_2^2: \ \hat y = y_i $$

Bayes Error

在一个分类问题中，使用任何算法所能达到的最小错误率

$$ P(error) = 1 - P(correct) = 1 - \int_{\mathcal{X}} P(correct|x)P(x)dx \\\ \\ \mathcal X是样本分布 \ \ P(correct): 正确分类的概率 $$

Regularization

Weight Dacay

$$ J(\pmb \omega) = MSE_{(train)} + \lambda\omega^T \omega \\\ \\ \lambda: Orthogonal \ parameter \\\ \\ \omega \uparrow \Longrightarrow J \uparrow \Longrightarrow 过拟合\downarrow $$

Regularizer

在Weight Decay中，$\pmb{\Omega(\omega) = \omega^T\omega}$
Regularization是通过优化模型降低其Generalization Error，而不是Test Error

Hyperparameters and Cross-Validation

Hyperparameters

训练前设置好的参数

Cross-Validation

定义

Cross-validation是一种评估机器学习模型性能的技术，它将数据集分成训练集和验证集，并使用不同的训练集和验证集组合来评估模型的性能。在交叉验证中，数据集被分成k个相等的子集，其中一个子集被保留用于验证模型，而其他k-1个子集被用于训练模型。这个过程重复k次，每次使用不同的子集作为验证集。最终，交叉验证会生成k个模型，每个模型都被评估一次，然后将这些评估结果的平均值作为模型的性能评估指标。

k-fold Cross-Variance Algorithm

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


def KFoldXV(D, A, L, k):
    # Require: D, the given dataset, with elements z (i)
    # Require: A, the learning algorithm, seen as a function that takes a dataset as input and outputs a learned function
    # Require: L, the loss function, seen as a function from a learned function f and an example z (i) ∈ D to a scalar ∈ R
    # Require: k, the number of folds
    # Split D into k mutually exclusive subsets D_i, whose union is D.

    n = len(D)
    fold_size = n // k # 整除运算符，向下取整
    folds = [D[i:i+fold_size] for i in range(0, n, fold_size)]
    errors = []

    for i in range(k):
        train_set = []
        for j, fold in enumerate(folds):
            if j != i:
                for z in fold:
                    train_set.append(z)

        f_i = A(train_set)

        for z in folds[i]:
            ej = L(f_i, z)
            errors.append(ej)

    return errors

Bias and Variance

Bias & MSE

$$ bias(\hat{\pmb \theta}_m) = \mathbb E(\hat{\pmb \theta}_m) - \pmb \theta \\\ \\ \begin{aligned} MSE &= \mathbb E[(\hat{\pmb \theta}_m - \pmb \theta)^2] \\ & = Bias^2(\hat{\pmb \theta}) + Var(\hat{\pmb \theta}) \end{aligned} $$

Supervised Learning Algorithm

Unsupervised Learning Algorithm

Principal Component Analysis (PCA)

详见Linear Algebra

K-means Clustering

$$ J(\theta) = \mathbb E $$

Gradient Descent

定义

不断地沿梯度方向前进,逐渐减小函数值的过程

迭代公式

$$ \theta = \theta - \alpha \nabla J(\theta) \\\ \\ \nabla J(\theta) = \begin{pmatrix} \frac{\partial J}{\partial \theta_1} \\ \frac{\partial J}{\partial \theta_2} \\ … \\ \frac{\partial J}{\partial \theta_n} \end{pmatrix} \\\ \\ \theta: 优化参数 \ \ \alpha:学习率 \ \ J: 目标参数 $$

学习率过大，结果会超大
学习率过小，结果几乎没有改变

思想

沿着梯度的负方向更新参数，求得函数的最小值

Challenges

计算资源和时间成本
数据偏差和公平性

Deep Learning

神经网络

图示

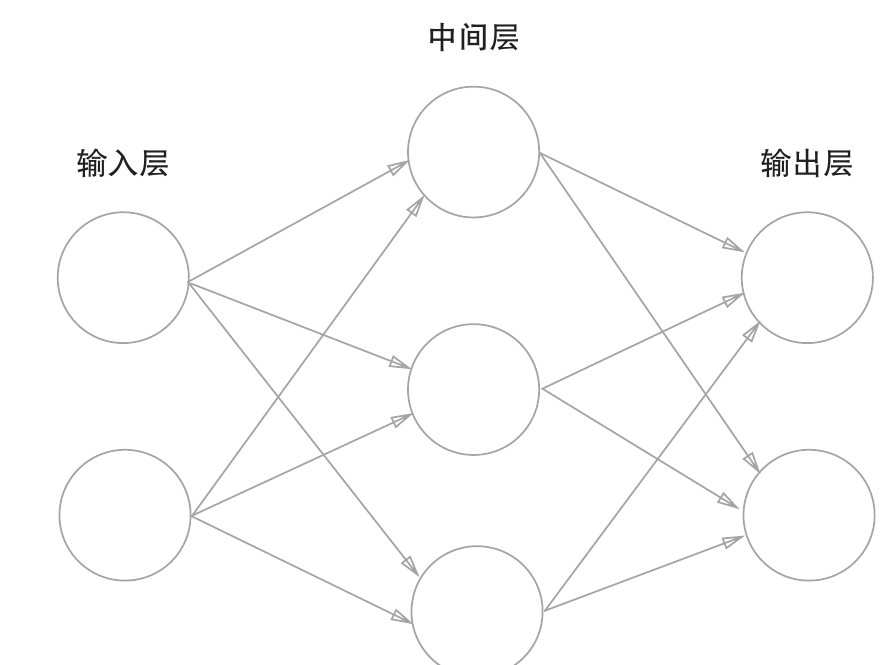
解释

中间层又被称为隐藏层
用第0,1,2层表示输入、中间、输出层

示例

图示——含有偏置的简单神经网络

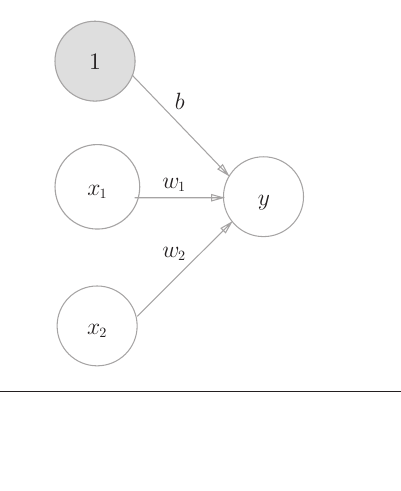
$$ y = \begin{cases} 0 & w_1x_1 + w_2x_2 + b \le 0 \\ 1 & w_1x_1 +w_2x_2 + b \gt 0 \end{cases} \\\ \\ 引入\pmb{激活函数h(x)}=\begin{cases} 1 & x\gt 0 \\ 0 & x\le 0 \end{cases} \\\ \\ 那么y = h(w_1x_1 + w_2x_2 + b) \\\ \\ 此处的激活函数是一种\pmb{阶跃函数} \\\ \\ \pmb{阶跃函数} 是感知机的激活函数 $$

进一步推导

图示

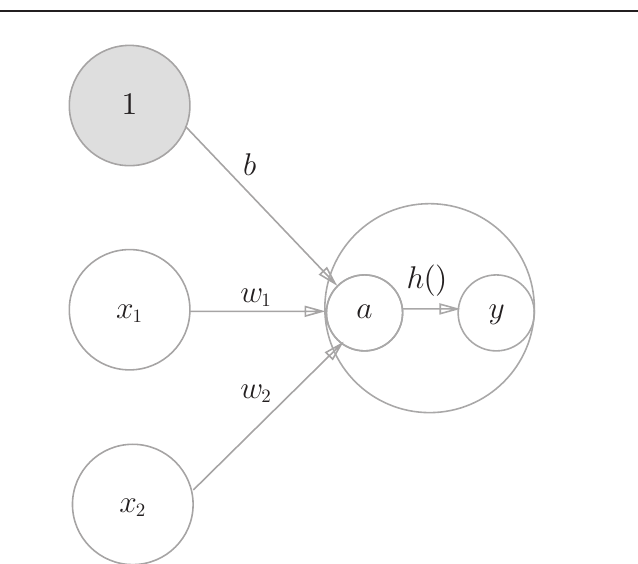
$$ a = w_1x_1 + w_2x_2 + b \\\ \\ y = h(a) $$

激活函数

sigmoid函数

$$ h(x) = \frac{1}{1+e^{-x}} $$

比较

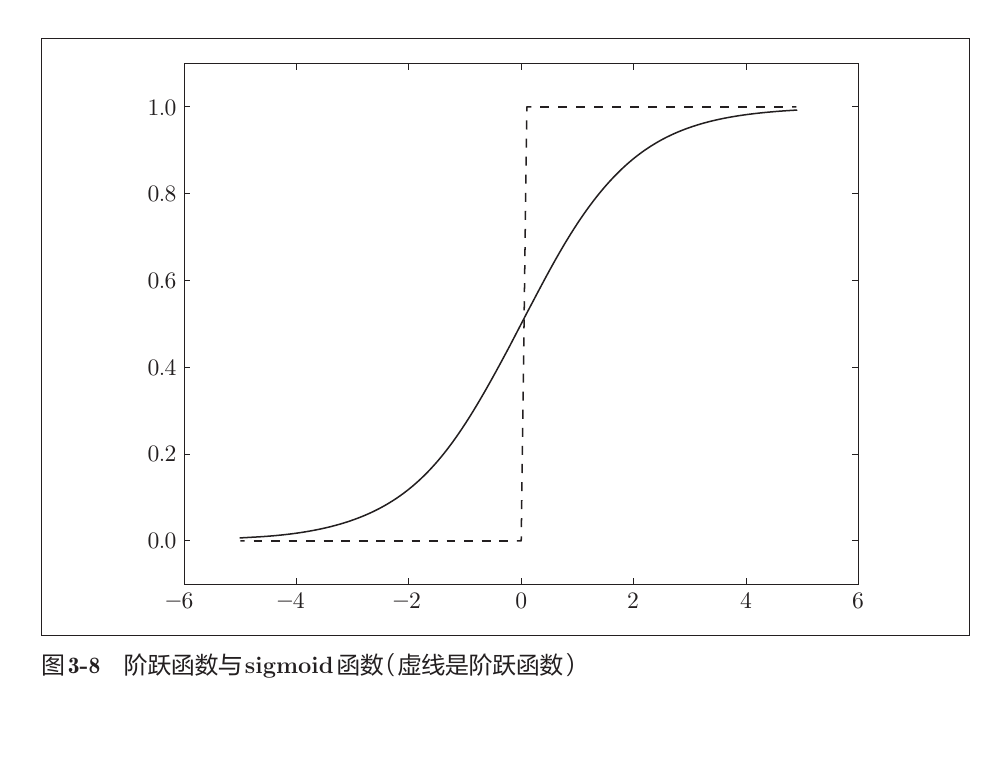
共同点

输出信号始终$\in(0,1)$
输入重要信息，输出较大的值
均为非线性函数

不同点

Sigmoid平滑，而阶跃函数突变

ReLU - Rectified Linear Unit

$$ h(x) = \begin{cases} x & x \gt 0 \\ 0 & x \le 0 \end{cases} $$

神经网络的内积

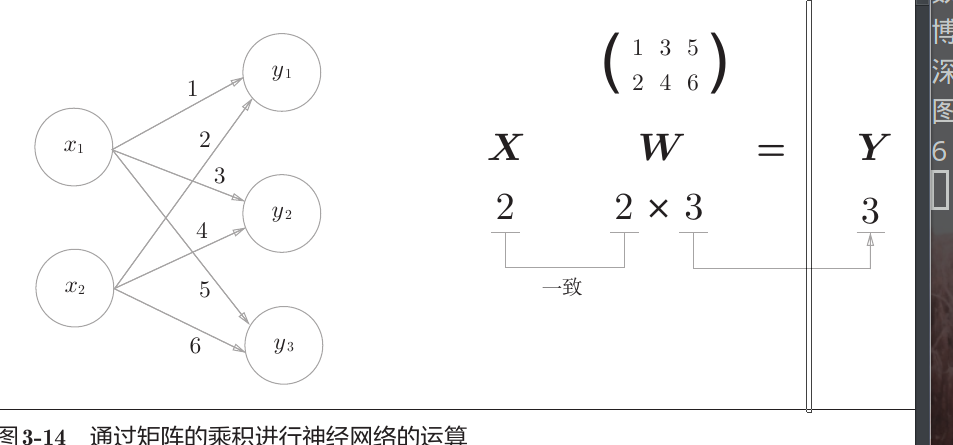
三层神经网络的实现

权重的符号

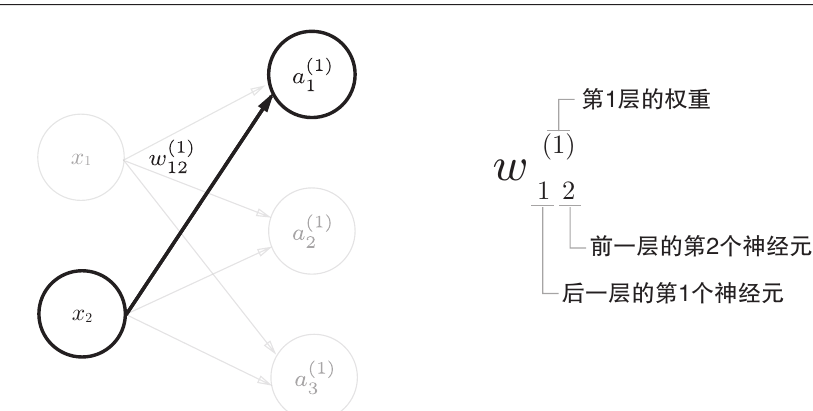
实现

$$ a_1^{(1)} = x_2w_{12}^{(1)} + x_1w_{11}^{(1)}+b_1^{(1)} \\\ \\ A^{(1)} = XW^{(1)} + B^{(1)} \\\ \\ 其中，A^{(1)} = \begin{pmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} \end{pmatrix} \\\ \\ X = \begin{pmatrix} x_1 & x_2 \end{pmatrix} \\\ \\ W^{(1)} = \begin{pmatrix} w_{11}^{(1)} & w_{21}^{(1)} & w_{31}^{(1)}\\ w_{21}^{(1)} & w_{22}^{(1)} & w_{23}^{(1)} \end{pmatrix} \\\ \\ B^{(1)} = \begin{pmatrix} b_1^{(1)} & b_2^{(1)} & b_3^{(1)} \end{pmatrix} $$

输出层的设计

回归问题 —— 恒等函数

$$ h(x) = x \ \ x \in R $$

上述代码总和

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104


import numpy as np
import matplotlib.pylab as plt

## 定义激活函数

def step_function(x):
    return np.array(x > 0, dtype=int)

def sigmoid(x):
    return 1/(1+np.exp(-x))

def ReLU(x):
    return np.maximum(0,x) ## 注意这个参数的使用

def identity(x):
    return x

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c) ## 溢出对策
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y

''' 函数绘制

## 绘制阶跃函数

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) ## 指定 y 轴的范围
plt.show()

## 绘制sigmoid函数

z = sigmoid(x)
plt.plot(x, z)
plt.ylim(-0.1, 1.1) ## 指定 y 轴的范围
plt.show()

## 绘制ReLU

w = ReLU(x)
plt.plot(x, w)
plt.ylim(-0.1, 6) ## 指定 y 轴的范围
plt.show()

'''

## 0-1层的信号传递

X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3]) ## 随机取特征、权重、偏差

A1 = np.dot(X, W1) + B1 ## 计算第一层A1

Z1 = sigmoid(A1) ## 计算A1的sigmoid函数

## 1-2层的信号传递

W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2]) ## 随机取权重和偏差

A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)

## 2-输出层的信号传递

W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])

A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3) ## 或者 Y = A3

## 整理

def init_network(): ## 权重和偏置的初始化
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    return network

def forward(network, x): ## 输入到输出方向的传递处理
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity(a3)
    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) ## [ 0.31682708 0.69627909]

神经网络的学习

损失函数

均方误差

$$ E = \sum_k\frac{1}{2}(y_k - t_k)^2 \\\ \\ t_k:训练数据 \ \ y_k:输出 \ \ k:维数 $$

交叉熵误差

$$ E = - \sum_k t_k \cdot ln(y_k) $$

mini-batch学习

定义

从大量数据中随机选取小批量数据进行学习

损失函数总和 (以交叉熵误差为例)

$$ E = -\frac{1}{N}\sum_k \sum_k t_{nk} \ ln(y_{nk}) $$

数学知识补充

数值微分

$$ \frac{df(x)}{dx} = \frac{f(x+h)-f(x-h)}{2h} \\\ \\ 通过\pmb{中心差分}实现更高的\pmb{精度} $$