Matrix
Category
Indentity & Inverse Matrix
$$ \begin{aligned} Ax &= b \\ AA^{-1} &= I_n \\ \therefore A^{-1} A x &= A^{-1}b \\ x & = A^{-1}b \end{aligned} $$
Orthogonal Matrix
- 定义
- 每一列彼此正交,均为单位向量
- 性质
-
$|Q| = \pm 1$
-
$||Q\textbf{x}||=||\textbf{x}||$
-
$\textbf{x}^T\textbf{y}=(Q\textbf{x})^T(Q\textbf{y})$
-
$Q = Q^T$
-
$QQ^T$也是正交矩阵
$AA^T$
-
对称矩阵
-
如果$A$是Square,那么$AA^T$是semidefinite
Linear Dependence & Span
Linear Combination
$$ Ax =b \Longrightarrow \sum_{i=1}^n{x_i} A = b \\ x,y是Ax=b的解 \Longrightarrow z = \alpha x + (1-\alpha) y 是Ax =b 的解 \\
$$
- 形如$\sum_{i=1}^n c_i x$的组合叫做 Linear Combination
Linear Indenpendence
- Definition
不能通过Linear Combination得到彼此的一组向量Linear Indenpendent
Singular Matrix
- Definition
- Square Matrix with Linear denpendent Columns
- 特征
-
Determinant = 0
-
没有Inverse Matrix
Norms
Definition
- 用于衡量矩阵的大小
$$ L^p \ norm: ||x||p = \Big( \sum{i=1}^n x_i^p \Big)^{\frac{1}{p}} $$
Category
- 1-Norm - 最大列
$$ ||A||1 = max{1\lt j \lt n}\sum_1^{m}|a_{ij}| $$
- Frobenius-Norm (2-Norm)
$$ \begin{aligned} ||A||2 &= \sigma{max}(A) \\ &= \sqrt{\sum_1^m\sum_1^n |a_{ij}|^2} \end{aligned} $$
- $\infin$-Norm - 最大行
$$ ||A||\infin = max{1\lt j \lt m}\sum_1^{n}|a_{ij}| $$
Property
-
$||x|| \gt 0$
-
$f(\pmb x) = 0 \Longrightarrow \pmb x =0$
-
$f(\pmb{x+y} ) \le f(\pmb x) + f(\pmb y)$
-
$\forall \alpha \in R, |\alpha| f(\pmb x) = f(\alpha \pmb x)$
Special Matrix and Vectors
Diagonal Matrix
- Definition
- A Square Matrix where all non-zero entries are on the diagonal
- Property
- $Determinant = \prod(Entries \ on \ the \ diagonal )$
Symetrical Matrix
$$ A = A^T \\\ \\ A = Q\Lambda Q^T \\\ \\ 其中,QQ^T = I (即Q与Q^T正交) $$
Unit Vector and Orthogonal Matrix
- Vector
$$ ||\pmb x||_2 = 1 \Longrightarrow \pmb x \ is \ a \ Unit \ Vector \\\ \\ \pmb{x^T y} = 0 \Longrightarrow x \ and \ y \ are \ \pmb{orthogonal} $$
- Matrix
$$ AA^T = A^T A =I \Longrightarrow A \ is \ a \ \pmb{Orthogonal \ Matrix} \\\ \\ \therefore A^T = A^{-1} $$
Decomposition
EigenDecomposition
Eigen Vector & Eigen Value
- Definition
$$ \pmb {Av} = \lambda \pmb v \\ \pmb v: eigenvector \\ \lambda: eigen \ value \\\ \\ \pmb{v^T A} = \lambda v^T \\ \pmb{v}: Left \ eigenvector $$
- Eigenvectors和EigenValues一一对应
- Property
- Scale
$$ \pmb {Av} = \lambda \pmb v \\\ \\ c\pmb {Av} = c\lambda \pmb v \\\ \\ \therefore \pmb v \ can \ be \ scaled $$
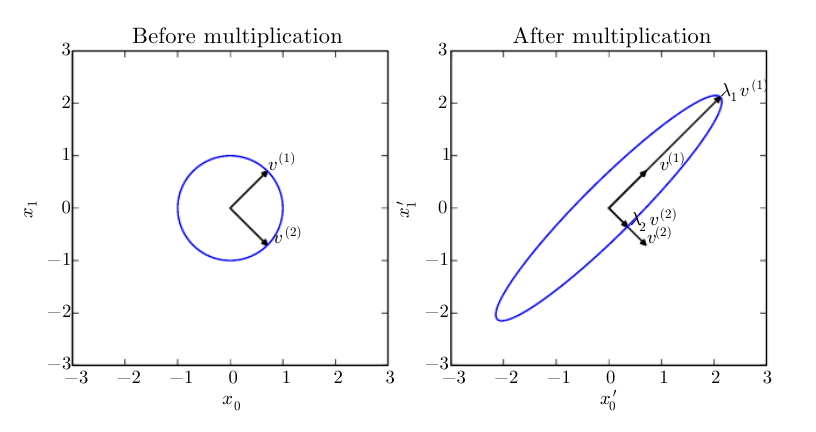
- EigenVaules
| All Positive | Positive definite |
|---|---|
| All Negative | Negative definite |
| All Non-zero | Positive semidefinite |
| All Negative | Negative semidefinite |
$$ Positive \ semidefinite \\ \forall \pmb x, \pmb {x^T A x} \ge 0 \\\ \\ Positive \ definite \\ \forall \pmb x \ \ \pmb{x^T A x} =0 \Longrightarrow \pmb x = 0 $$
- Solution
$$ \begin{aligned} \pmb{Av} &= \lambda \pmb v \\ \pmb{Avv^T} &= \lambda \pmb{vv^T} \\ \pmb{A} &= \lambda \pmb I \\ |\pmb A - \lambda \pmb I| &= 0 \end{aligned} $$
EigenDecomposition
- 前提
-
所有独立的$\pmb v$形成一个特征矩阵$\pmb V = (v^{1} , … v^{n})$
-
所有对应的特征值形成一个对角矩阵$diag(\pmb \lambda)$
- 分解
$$ \begin{aligned} \pmb{AV} &= \pmb{V diag(\lambda)} \\ EigenDecomposition: \pmb{A} &= \pmb{Vdiag(\lambda) V^{-1}} \end{aligned} $$
- Symetrical Matrix
-
主对角线两侧的元素关于主对角线对称
-
$A = A^T$
-
$A$的特征矩阵$Q$是一个正交矩阵
-
EigenDecomposition: $\pmb {A = Q\Lambda Q^T}(A和Q是Similar \ Matrix)$
Singular Value Decomposition
$$ \pmb{A = UDV^T} \\\ \\ U 和V都是orthogonal \ matrix \\\ \\ D是 diagonal \ matrix $$
-
Columns of U: Left-Singular Vectors(eigenvector of $AA^T$)
-
Columns of V: Right-Singular Vectors(eigenvectors of $A^TA$)
-
D的主对角线的元素是A的Singular Value($A^T A或AA^T$的EigenVaules的平方根)
Pseudoinverse & Trace Operator
Pseudoinverse
Definition
$$ A^+ = \underset{\alpha \searrow 0}{lim} \ (A^T A + \alpha I)^{-1}A^T \\\ \\ 非奇异矩阵: A^+ = A^{-1} \\\ \\ 奇异矩阵: A^+= (A^TA)^{-1}A^T \\\ \\ m \gt n: A^+= (A^TA)^{-1}A^T \\\ \\ n \gt m: A^+ = A^T(A^TA)^{-1} $$
Computing Algorithms
$$ A^+ = VD^+U^T (Singular \ Decomposition)\\\ \\ D^+: 对D元素取倒数 $$
Trace Operator
Definition
$$ Tr(\pmb A) = \sum_{i}A_{i,i} $$
Property
- Norm Computing
$$ ||\pmb A||_F = \sqrt{Tr(\pmb{AA^T})} $$
- Equality
$$ Tr(\pmb A) = Tr(\pmb A^T) $$
- Scalar
$$ Tr(a) = a $$
- Matrix
$$ Tr(\pmb{ABC}) = Tr(\pmb{CAB}) = Tr(\pmb{BAC}) $$
Principal Components Analysis
实现
$$ \lbrace \pmb{x^{(1)}…x^{(m)}} \rbrace \\\ \\ Encoder: \ f(\pmb x) = \pmb c \\\ \\ Decoder: \pmb x \approx g(\pmb c) = \pmb{Dc} \\\ \\ \pmb D是正交矩阵\\\ \\ L^ 2\ norm: \pmb c^* = \underset{c}{arg \ min} ||\pmb x-g(\pmb c)||_2 \\\ \\ L^2 \ norm \ge 0 \underset{为了方便计算}{\Longrightarrow} \pmb c^* = \underset{c}{arg \ min} ||\pmb x-g(\pmb c)||2^2 \\\ \\ \begin{aligned} \pmb c^* &= |\pmb x-g(\pmb x)|^T|\pmb x-g(\pmb x)| \\ &= x^Tx - x^Tg(c) - g^T(c)x + g^T(x)g(c) \\ &= 无关项 -2x^Tg(c) + g^T(c)g(c) \\ &= 无关项 -2x^T Dc + c^TD^TDc \\ &= 无关项 -2x^TDc + c^Tc \\\ \\ \nabla{\pmb c}(-2x^TDc + c^Tc) &= 0 \\ -2D^Tx +2c &=0 (疑问!!!) \\ c &= D^T x \end{aligned} \\\ \\ 于是f(x) = D^Tx $$
方差
$$ Var(x) = \frac{1}{m-1}\pmb{X^TX} \\\ \\ \pmb{X^TX} = \pmb{W\Lambda W^T} \\\ \\ \pmb X = \pmb{U\Sigma W} \\\ \\ \begin{aligned} \therefore \pmb{X^TX} &= \pmb{(U\Sigma W)^T(U\Sigma W)} \\ &= \pmb{W\Sigma^2W^T} \end{aligned} \\\ \\ Var(\pmb x) = \frac{1}{m-1}\pmb {X^TX} \\\ \\ if \ \pmb{z = x^TW} \\\ \\ Var[\pmb z] = \frac{1}{m-1} \Sigma^2 $$
适用情况
-
数据集包含多个变量,需要降低维度以简化数据。
-
变量之间存在高度相关性,需要将它们转换为更少的无关变量。
-
需要识别数据集中最重要的因素或特征。
-
需要可视化数据集并找到潜在的模式和关系。