并联RLC固有响应
图示
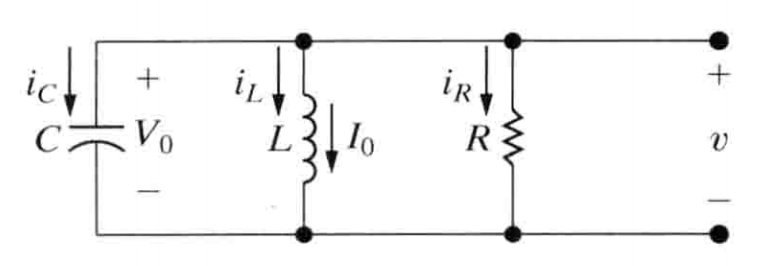
推导
$$ \frac{v}{R} +\frac{1}{L}\int_0^t vd\tau + I_0 + C\frac{dv}{dt} = 0 \\\ \\ 对t取微分得到:\frac{1}{R}\frac{dv}{dt} + \frac{v}{L} + C\frac{d^2v}{dt^2} = 0 \\\ \\ 整理得: \frac{d^2 v}{dt^2} + \frac{1}{RC}\frac{dv}{dt} +\frac{v}{LC} = 0 [1] $$
回顾二次微分方程的解法
$$ 假设 v = A e ^{st} \\\ \\ 代入[1]式可以得到: Ae^{st} (s^2 + \frac{s}{RC} + \frac{1}{LC}) = 0 \\\ \\ 解s^2 + \frac{s}{RC} + \frac{1}{LC} = 0 \\\ \\ 得 s_1 = -\frac{1}{2RC} + \sqrt{(\frac{1}{2RC})^2 - \frac{1}{LC}} \\\ \\ s_2 = -\frac{1}{2RC} - \sqrt{(\frac{1}{2RC})^2 - \frac{1}{LC}} \\\ \\ 最终得到 v = A_1 e^{s_1 t}+A_2 e ^{s_2 t } \\\ \\ 改写s_1,s_2 \\\ \\ s_1 = -\alpha + \sqrt{\alpha^2 - \omega_0^2} \\\ \\ s_2 = -\alpha - \sqrt{\alpha^2 - \omega_0^2} \\\ $$
- 固有响应参数
| 参数 | 名称 | 取值 |
|---|---|---|
| $s_1,s_2$ | 特征根 | 如上 |
| $\alpha$ | 奈培频率 | $1/2RC$ |
| $\omega_0$ | 谐振角频率 | $1/\sqrt{LC}$ |
- 响应分类
-
若为两个不同的实根,则为过阻尼响应
-
若为两个相同的实根,则为临界阻尼响应
-
若为两个共轭复数根,则为欠阻尼响应
并联RLC电路固有响应的形式
过阻尼响应
- 通过解
$$ v(0^+) = A_1 + A_2 \\\ \\ \frac{dv(0^+)}{dt} = \frac{i_C(0^+)}{C} = s_1A_1 + s_2 A_2 $$
- 得到$A_1,A_2$的值,进而得到$v$的值
欠阻尼响应
-
求解 $$ 令\omega_d = \sqrt{\omega_0^2 - \alpha^2} \\\ \\ v(t) = A_1 e^{(-\alpha + j\omega_d)t} + A_2e^{(-\alpha - j\omega_d)t} \\\ \\ = e^{-\alpha t}(A_1 cos\omega_d t + j A_1 sin\omega_d t + A_2cos\omega_d t - jA_2 sin\omega_d t) (使用欧拉公式)\\\ \\ = e^{-\alpha t} [(A_1 + A_2)cos\omega_d t + (A_1-A_2)sin\omega_d t] \\\ \\ 令B_1 = A_1+A_2, B_2 = A_1 - A_2 \\\ \\ v(t) = e^{-\alpha t} (B_1cos\omega_d t + B_ 2sin\omega_d t) \\\ \\ 进而得到 \\\ \\ \pmb{v(0^+)= B_1} \\\ \\ \pmb{\frac{dv(0^+)}{dt} = \frac{i_c(0^+)}{C} =-\alpha B_1 + \omega_d B_2} $$
-
特性
-
欠阻尼系统中,响应是振荡的
-
过阻尼系统里,响应趋近于一个最终值
临界阻尼响应
$$ \because s_1 =s_2 =\alpha \\\ \\ \therefore v(t) = D_1 t e^{-\alpha t} + D_2 e^{-\alpha t} \\\ \\ v(0^+) = D_2 \\\ \\ \frac{dv(0^+)}{dt} = D_1 - \alpha D_2 $$
并联RLC阶跃响应
图示
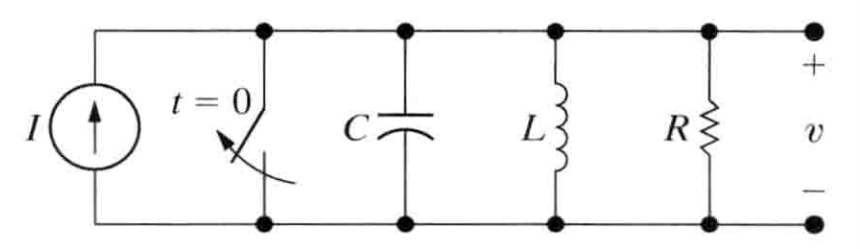
电路的二次微分方程
$$ I = C\frac{dv}{dt} + i_L + \frac{v}{R} \\\ \\ 其中, v =L\frac{di}{dt},\frac{dv}{dt} = L\frac{d^2 i }{dt^2} \\\ \\ 代入上式并整理得 \\\ \\ \frac{d^2i_L}{dt^2} + \frac{1}{RC} \frac{di_L}{dt} + \frac{i_L}{LC} = \frac{I}{LC} $$
串联RLC的固有响应和阶跃响应
固有响应
图示
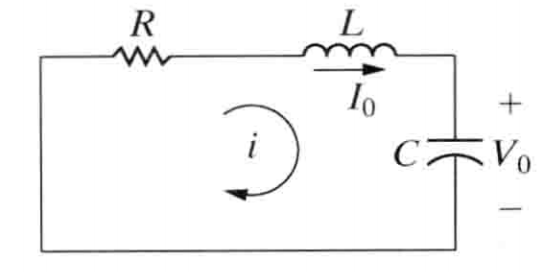
结果
$$ 过阻尼: i(t) = A_1e^{s_1t} + A_2 e^{s_2 t} \\\ \\ 欠阻尼: i(t) = B_1e^{-\alpha t} cos\omega_d t + B_ 2e^{-\alpha t} sin\omega_d t \\\ \\ 临界阻尼: i(t) = D_1 t e^{-\alpha t} + D_2 e^{-\alpha t} \\\ \\ 其中,奈培频率 \alpha = \frac{R}{2L} \\\ \\ 谐振角频率 \omega_0 =\sqrt{\frac{1}{LC}} $$
双集成运放电路
两级联运算放大器
图示
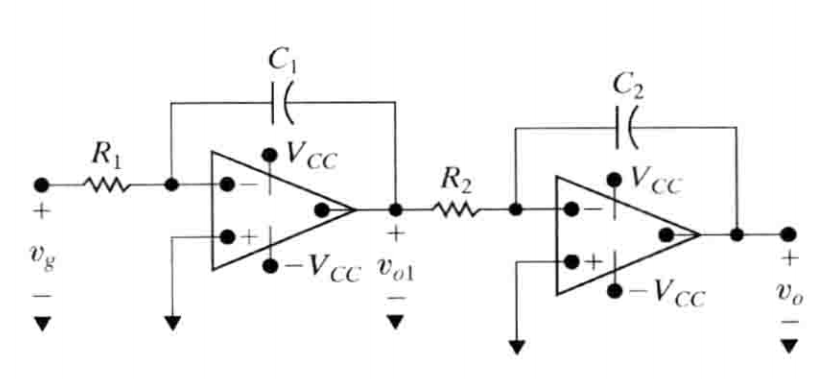
输入输出电压关系
$$ 对于第一个反相输入端 \\\ \\ \frac{0-v_g}{R_1}+ C\frac{d(0-v_{o1})}{dt} = 0 \Rightarrow \frac{dv_{o1}}{dt} = -\frac{1}{R_1C_1}v_g \\\ \\ 同理: \frac{dv_{o2}}{dt} = - \frac{1}{R_2C_2}v_g \\\ \\ \therefore \frac{d^2v_{o2}}{dt^2} = \frac{1}{R_1C_1}\frac{1}{R_2C_2}v_g $$
具有反馈电阻的两级运算放大电路
图示
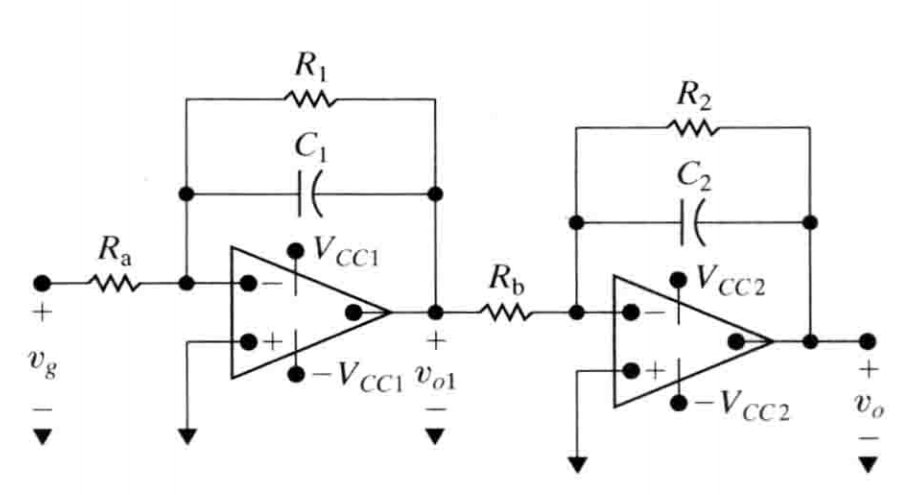
输入输出电压关系
$$ 对于第一个反相输入端 \\\ \\ \frac{0-v_g}{R_a} + \frac{0-v_{o1}}{R_1}+ C\frac{d(0-v_{o1})}{dt} = 0 \\\ \\ \frac{dv_{o1}}{dt} + \frac{v_{o1}}{C_1R_1}= -\frac{v_g}{C_1R_a} \\\ \\ 同理: \frac{dv_o}{dt} +\frac{v_{o}}{C_2R_2} =-\frac{v_g}{C_1R_b} \\\ \\ 令\tau_1 = R_1C_1 , \tau_2 = R_2C_2 \\\ \\ 对上式去微分,可以得到 \\\ \\ \frac{d^2v_o}{dt^2} + (\frac{1}{\tau_1}+\frac{1}{\tau_2})\frac{dv_o}{dt} +\frac{1}{\tau_1\tau_2}v_o = \frac{v_g}{R_aC_1 R_bC_2} \\\ \\ 解方程得其特征根为 \\\ \\ s_1 = -\frac{1}{\tau_1},s_2 = -\frac{1}{\tau_2} $$